Introduction to Diffusion Models
May 27, 2024 | min | Jean-Baptiste Bouvier
Diffusion models have reached state-of-the-art performance in terms of image and video generation. Thus, most of the models available online focus on these difficult tasks which require complex code inaccessible to the novice. Instead, in this post I will focus on the implementation of a simple diffusion model in Python in just 100 lines of code! This mininal implementation makes understanding diffusion models much easier! All the codes mentioned in this post are available on GitHub.
What are diffusion models?
Diffusion models belong to the class of generative machine learning as they can create new content. In short, diffusion models learn to iteratively remove noise from the data until obtaining a clean sample. The generation process starts from a purely stochastic signal, a white noise. Then, a trained diffusion model can iteratively decrease the noise level of this data until converging to a sample of a desired distribution (for instance images of bikes).
There are plenty of good resources explaining in great detail how diffusion models work, such as Lilian Weng's blog post or even Wikipedia. However, the understanding brought by these excellent resources is not enough to actually code a diffusion model. Here I will focus on extremely simple models allowing to understanding how to code your first diffusion model.
How to implement a diffusion model in 100 lines of Python?
The simplest diffusion code is simple_1Diffusion.py,
which you can find in the codes folder of the GitHub repo.
This code implements a basic diffusion model for 1D data and is self-contained in 100 lines of Python!
Libraries
In this simplest implementation, the only extra libraries to install are torch for the neural networks, matplotlib for plotting our results, and numpy for the calculations.
import torch import random import numpy as np import torch.nn as nn import matplotlib.pyplot as plt
Data distribution
The data distribution to be generated is a Gaussian of mean mu_data and standard deviation (std) sigma_data.
mu_data = 1.
sigma_data = 0.01 The goal will be to recover this data distribution from a unit Gaussian noise of mean $\mu_{noise} = 0$ and std $\sigma_{noise} = 1$ as illustrated below.
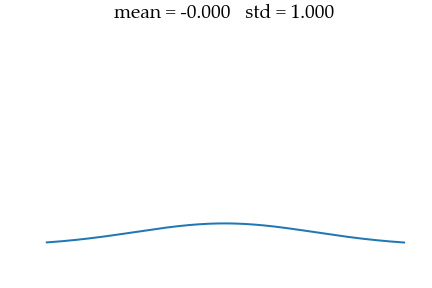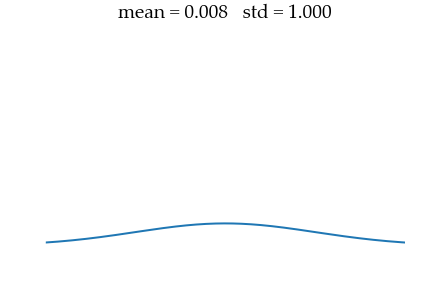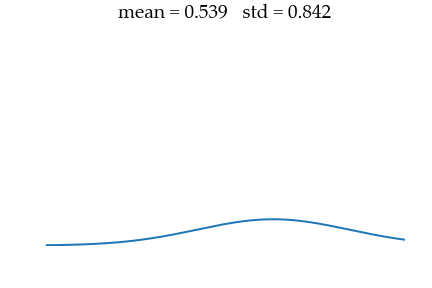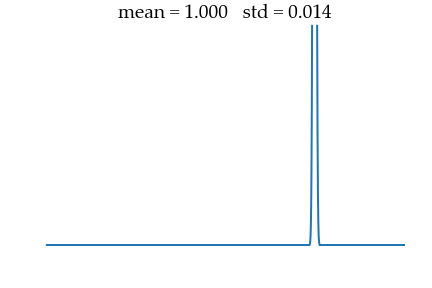
Hyperparameters
Training of the denoiser neural network (dnn) will use a learning rate lr and iterate for 1000 epochs.
We define the minimal and maximal std of the noise levels of the dnn sigma_min and sigma_max.
These noise levels Sigmas are spread following a log-normal scale as suggested by the paper
"Elucidating the Design Space of Diffusion-Based Generative Models".
The test_size describes the number of datapoints to be denoised after training.
lr = 1e-3
batch_size = 32
nb_epochs = 1000
sigma_min = sigma_data/10
sigma_max = 1.
N = 10 # number of noise scales
rho = 7 # log normal scale
Sigmas = (sigma_max**(1/rho) + torch.arange(N)*(sigma_min**(1/rho) - sigma_max**(1/rho))/(N-1))**rho
Sigmas = torch.cat((Sigmas, torch.tensor([0.])), dim=0)
test_size = 1000 Denoiser
The dnn is coded using the class Denoiser with a neural network taking as inputs the data x and its noise level sigma
before returning its prediction of the noise to be removed.
We use a simple Multi-Layer Perceptron with ReLU activations as our neural network.
class Denoiser(nn.Module):
def __init__(self, width):
super().__init__()
self.net = nn.Sequential(nn.Linear(1+1, width), nn.ReLU(),
nn.Linear(width, width), nn.ReLU(),
nn.Linear(width, 1) )
def forward(self, x, sigma):
s = sigma*torch.ones_like(x)
return self.net( torch.cat((x, s), dim=1) )
denoiser = Denoiser(32) Training
The training loop randomly chooses a noise level sigma and creates a noise signal n to be added to
the clean data y of mean mu_data and std sigma_data.
The dnn denoiser takes as inputs the noised data y + n and its noise level sigma.
The dnn is trained to predict the extra noise corresponding to a transition between levels Sigmas[i] and Sigmas[i+1].
We calculate a quadratic loss and use stochastic gradient descent (SGD) to optimize the denoiser.
Finally, we plot the evolution of the training loss over the epochs.
losses = np.zeros(nb_epochs)
optimizer = torch.optim.SGD(denoiser.parameters(), lr)
for epoch in range(nb_epochs):
id_sigma = random.randint(0, N-1)
sigma = Sigmas[id_sigma]
y = torch.randn((batch_size,1))*sigma_data + mu_data
n = torch.randn_like(y)*sigma
pred = denoiser(y + n, sigma)
loss = torch.sum( (pred - n*Sigmas[id_sigma+1]/sigma )**2 )
optimizer.zero_grad()
loss.backward()
optimizer.step()
losses[epoch] = loss.detach().item()
plt.title("Training loss")
plt.plot(np.arange(nb_epochs), losses)
plt.show() Denoising
The denoising process starts from a stochastic signal x of mean 0 and std sigma_max.
From this signal we iteratively remove one noise level using the trained dnn until obtaining a cleaned signal corresponding to
the initial data distribution of mean mu_data and std sigma_data.
x = torch.randn((test_size, 1))*sigma_max
print(f"Noised sample: mean {x.mean().item():.3f} std {x.std().item():.3f}")
Mean, Std = np.zeros(N+1), np.zeros(N+1)
Mean[0], Std[0] = x.mean().item(), x.std().item()
for i in range(N):
with torch.no_grad():
x -= denoiser(x, Sigmas[i])
Mean[i+1], Std[i+1] = x.mean().item(), x.std().item()
print(f"Denoised sample: mean {x.mean().item():.3f} std {x.std().item():.3f}")
print(f"Denoising goal: mean {mu_data:.3f} std {sigma_data:.3f}")
You can now run this code and verify that the Denoiser can actually generates the initial data distribution from a random sample.
We can even make a video of this quick denoising process with
simple_1Diffusion_video.py.
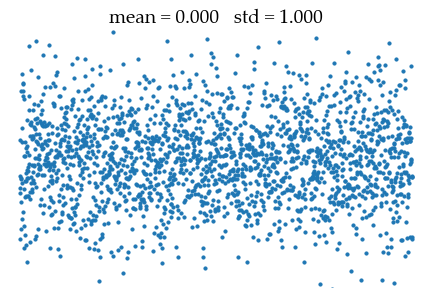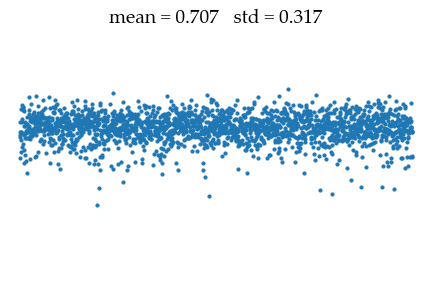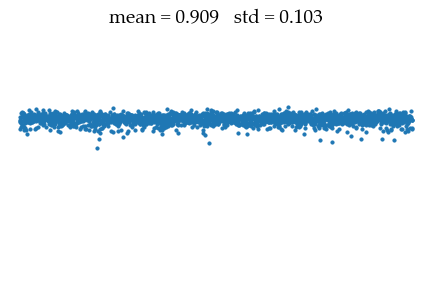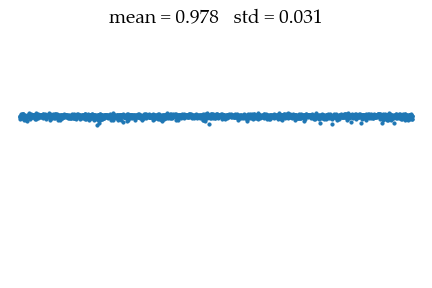
into the data distribution of mean $\mu_{data} = 1$ and std $\sigma_{data} = 0.01$.
Diffusion models in 2D
Now that we have a 1D denoiser, we can scale it up to 2D with minimal changes and obtain the code
simple_2Diffusion.py.
Diffusion models are supposed to be very expressive, allowing them to capture multimodalities present in the initial data. We will illustrate this with an initial data distribution being the sum of 4 narrow Gaussians with spikes at $(-1, -1)$, $(-1, 1)$, $(1, -1)$, and $(1, 1)$. As before, we will add noise until this initial distribution is indistinguishable from a Gaussian centered at the origin with std 1. The denoising process should then separate the data into the four spikes as illustrated on the gif below.

The code to implement this 2D multimodal diffusion process is
simple_multimodal.py
and the gif can be generated with simple_multimodal_video.py.
Denoising Diffusion Probabilistic Models (DDPM)
The diffusion models presented so far use a naive denoising process which works on our simple cases.
To obtain better quality diffusion models we will follow the implementation of "Denoising Diffusion Probabilistic Models" (DDPM).
The simplest code for 1D data is single_DDPM.py.
Note that single_DDPM.py uses a single neural network to denoise each noise level, but we could also have one neural network for each noise level as implemented in simple_DDPM.py.
As we did previously, we can also extend DDPM to 2D multimodal data distributions with the code
multimodal_DDPM.py.
Finally, to get a better understanding of the evolution of the probability density functions (pdf) through the different noise scales you can look at
detailed_DDPM.py.
Quick Summary
- Diffusion models learn to iteratively remove noise.
- A trained diffusion model generates new data by denoising some random initial data.
- We implemented a simple diffusion model in 100 lines of Python!
References
-
Jonathan Ho, Ajay Jain, and Pieter Abbeel, Denoising diffusion probabilistic models, Advances in Neural Information Processing Systems, pages 6840 - 6851, 2020.
-
Tero Karras, Miika Aittala, Timo Aila, and Samuli Laine, Elucidating the Design Space of Diffusion-Based Generative Models, Advances in Neural Information Processing Systems, pages 26565 - 26577, 2022.