Understanding resilience
June 15, 2023 | min | Jean-Baptiste Bouvier
Table of contents
I developped resilience theory during my PhD to study how autonomous systems can handle a loss of control authority over some of their actuators. Let's start with a few scenarios illustrating such a malfunction.
On July 29 2021, after the Nauka module docked to the International Space Station (ISS), a software failure caused a misfire of all the module's thrusters (Bartels 2021). As a result, the whole station lost attitude control for 15 minutes and rotated by 540$^\circ$ possibly endangering the ISS crew. Eventually, other thrusters on the ISS were fired to counteract the uncontrolled and undesirable thrust until the Nauka module ran out of fuel.

(Image credit: Thomas Pesquet/ESA/NASA)
Autonomous systems’ malfunctions are not always accidental as in the previous scenario, they can also be caused purposefully by adversarial attacks. Indeed, control systems are increasingly connected to the Internet (Fawzi et al. 2014), and hence they are more prone to cyber attacks. A well documented example is the attack on the Maroochy sewage control system in Australia (Fawzi et al. 2014), where a disgruntled ex-employee took remote control over sewer valves and managed to flood a hotel, a park and a river with a million liters of sewage.
Framework
Motivated by these accidental and orchestrated failures, my PhD thesis investigated the guaranteed resilience of autonomous systems in the face of such malfunctions. We define a loss of control authority over actuators as a malfunction characterized by some actuators producing uncontrolled and undesirable outputs instead of following the controller’s commands. A loss of control authority can be caused, for instance, by a software bug as in the ISS example or by an adversarial takeover of actuators as in the sewage example.
After such a malfunction a Fault Detection and Isolation (FDI) module identifies the faulty actuators thanks to real-time readings of each actuator's output (Amin et al. 2019). Then, the design of a controller operating in such off-nominal conditions would classically rely on robust control, adaptive control (Wang et al. 2001), or fault-tolerant control (Amin et al. 2019). However, robust control needs the undesirable inputs to be significantly smaller than the controls to provide meaningful results (Wang et al. 2001), which is not the case here. On the other hand, the estimators of adaptive control are designed to adapt to unknown constant parameters and not to uncontrolled inputs likely to vary at much faster timescales (Wang et al. 2001). Finally, fault-tolerant control after actuator malfunctions mostly covers partial loss of effectiveness for controllable actuators or locked-in-place actuators (Amin et al. 2019), and not uncontrolled actuators. Therefore, a new control theory was needed to investigate loss of control authority over actuators.
We consider a system of state $x(t)$ and nominal dynamics \begin{equation}\label{eq: framework ODE} \dot{x}(t) = f\big(t, x(t)\big) + g\big(t, x(t)\big) \bar{B} \bar{u}(t), \qquad x(0) = x_0 \in \mathbb{R}^n, \end{equation} with constant matrix $\bar{B} \in \mathbb{R}^{n \times (m+p)}$ and control signal $\bar{u}(t) \in \bar{\mathcal{U}}$.
After a loss of control authority, $p$ of the initial $m+p$ actuators of the nominal system are now producing uncontrolled and possibly undesirable outputs within their full actuation range. We split $\bar{B}$ between the controlled actuators $B$ and the malfunctioning ones $C$. Similarly, nominal signal $\bar{u}$ is split between the controls $u(t) \in \mathcal{U}$ and the undesirable inputs $w(t) \in \mathcal{W}$. The malfunctioning dynamics become \begin{equation}\label{eq: framework split ODE} \dot{x}(t) = f\big(t, x(t)\big) + g\big(t, x(t)\big) \big(Bu(t) + Cw(t) \big), \qquad x(0) = x_0 \in \mathbb{R}^n. \end{equation} The loss of control authority is clearly illustrated by the fact that the controller only chooses $u(t)$, while the undesirable input $w(t)$ is determined by other uncontrolled factors.
As discussed previously, the sensors of the FDI module provide real-time measurements of the malfunctioning actuators’ outputs $w(t)$ to the controller. Thus, the command $u(t)$ can be adapted in a reactive fashion to $w(t)$. Thanks to additional sensors like GPS, cameras, radars, etc, the controller has also a perfect knowledge of the state $x(t)$. To illustrate this knowledge, we write $u(t) = u\big(t, x(t), w(t) \big)$.
Because of the loss of control authority, malfunctioning system \eqref{eq: framework split ODE} might not be able to complete the nominal mission assigned before the malfunction. We first consider simple missions of target reachability. Let $\mathcal{T}$ be a target set that we assume to be reachable by nominal system \eqref{eq: framework ODE}, i.e., there exists a control $\bar{u}$ driving the state of \eqref{eq: framework ODE} from $x_0$ to $x(T_N) \in \mathcal{T}$ in some time $T_N \geq 0$.
For the malfunctioning system, we need a slightly different notion of reachability, because it should not depend on $w$. Target $\mathcal{T}$ is resiliently reachable if for every signal $w$ there exists a control $u$ driving the state of \eqref{eq: framework split ODE} from $x_0$ to $x(T_M) \in \mathcal{T}$ in some time $T_M \geq 0$. The main obstacle preventing resilient reachability is the actuation constraint $u(t) \in \mathcal{U}$ that might prevent the controller from overcoming some undesirable inputs $w$ and adequately steering the state to $\mathcal{T}$.
Problem 1: Under what conditions is a target $\mathcal{T}$ resiliently reachable by malfunctioning system \eqref{eq: framework split ODE}?
Solving Problem 1 gives a method to study the remaining capabilities of a system that has suffered a partial loss of control authority over its actuators. When studying safety-critical systems, such a post-failure analysis should conclude that the malfunctioning system is still capable of completing its nominal mission. Therefore, safety-critical systems must be designed resilient to a partial loss of control authority over their actuators. This train of thoughts leads us to our second problem of interest.
Problem 2: How to design a system resilient to the loss of control over any one of its actuators?
Resilience only requires that target set $\mathcal{T}$ remains reachable by malfunctioning system \eqref{eq: framework split ODE} in some finite time $T_M$. After an extremely damaging loss of control, $T_M$ could be several orders of magnitude larger than $T_N$, the nominal reach time for system \eqref{eq: framework ODE}. This can prevent mission completion if $T_M$ is too large. For instance, a drone could run out of battery or a spacecraft run out of fuel before reaching the target. Our third objective is then to quantify the resilience of the system by estimating the maximal time penalty caused by the loss of control authority.
Problem 3: How to quantify the resilience of control systems?
We will now see how to solve these three problems as I did during my PhD.
Resilient Reachability of Linear Driftless Systems (Bouvier et al., 2020)
Let us start by considering simple linear dynamics \begin{equation}\label{eq: ODE} \dot x(t) = Ax(t) + \bar{B} \bar{u}(t), \qquad x(0) = x_0 \in \mathbb{R}^n, \end{equation} where $A \in \mathbb{R}^{n \times n}$ and $\bar{B} \in \mathbb{R}^{n \times (m+p)}$ are constant matrices. After a loss of control authority over $p$ of the $m+p$ actuators, we split $\bar{B}$ and $\bar{u}$ as before to obtain the malfunctioning dynamics \begin{equation}\label{eq: split} \dot x(t) = Ax(t) + Bu(t) + Cw(t), \quad x(0) = x_0 \in \mathbb{R}^n, \quad u(t) \in \mathcal{U}, \quad w(t) \in \mathcal{W}. \end{equation} We consider the admissible inputs to be square integrable signals over their time domain $[0, T]$, \begin{equation*} \mathcal{F}(\mathcal{U}) := \big\{u \in \mathcal{L}_2\big([0, T], \; \mathcal{U} \big) : \|u\|_{\mathcal{L}_2} \leq 1 \big\}, \qquad \mathcal{F}(\mathcal{W}) := \big\{w \in \mathcal{L}_2\big([0, T], \; \mathcal{W} \big) : \|w\|_{\mathcal{L}_2} \leq 1 \big\}. \end{equation*} Systems with such input bounds are typically refered to as energy bounded. The target set $\mathcal{T}$ is the ball of radius $\varepsilon$ around $x_{goal} \in \mathbb{R}^n$, $\mathcal{T} := \mathbb{B}(x_{goal}, \varepsilon)$.
Simplifying the adjoint maps of the reachability condition from (Delfour et al. 1969) leads to our first resilience condition. Target set $\mathcal{T}$ is resiliently reachable at time $T$ by system \eqref{eq: ODE} if and only if \begin{equation}\label{eq:thm2} \hspace{-12mm} \underset{h\, \in\, \mathbb{S}}{\max} \Bigg\{ \hspace{-1mm} \langle h, e^{AT}x_0 - x_{goal} \rangle - \hspace{-2mm} \underset{\|u\|_{\mathcal{L}_2} = 1}{\sup} \hspace{-1mm} \left\{ \hspace{-0.5mm} \Big|\Big\langle h, \hspace{-1mm} \int_0^T \hspace{-4mm} e^{A(T-\tau)}B u(\tau) d\tau \Big\rangle\Big| \hspace{-0.5mm} \right\} + \hspace{-2mm} \underset{\|w\|_{\mathcal{L}_2} = 1}{\sup} \hspace{-1mm} \left\{ \hspace{-0.5mm} \Big|\Big\langle h, \hspace{-1mm} \int_0^T \hspace{-4mm} e^{A(T-\tau)}C w(\tau) d\tau \Big\rangle\Big| \hspace{-0.5mm} \right\} \hspace{-1mm} \Bigg\} \leq \varepsilon. \end{equation}
To further simplify \eqref{eq:thm2}, we consider the linear driftless nominal dynamics \begin{equation}\label{eq:driftless} \dot{x}(t) = \bar{B} \bar{u}(t), \qquad x(0) = x_0 \in \mathbb{R}^n, \qquad \bar{u}(t) \in \bar{\mathcal{U}}. \end{equation} After a loss of control authority over actuators, the malfunctioning dynamics become \begin{equation}\label{eq:driftless split} \dot{x}(t) = Bu(t) + Cw(t), \quad x(0) = x_0 \in \mathbb{R}^n, \quad u(t) \in \mathcal{U}, \quad w(t) \in \mathcal{W}. \end{equation} Nominal system \eqref{eq:driftless} is resilient if any target is resiliently reachable by malfunctioning system \eqref{eq:driftless split}. We can show that resilience is equivalent to $BB^\top - CC^\top \succ 0$, which is significantly easier to verify than condition \eqref{eq:thm2}.
Now that we have solved Problem 1 for linear systems with bounded energy, let us investigate Problem 2 and the question of resilient system design.
Designing Resilient Linear Systems (Bouvier et al., 2022)

For the linear driftless dynamics \eqref{eq:driftless}, a system in dimension $n$ needs at least $2n+1$ actuators to be resilient to the loss of control over any one of them. The intuition behind this minimal size result is easily understandable on the following example of resilient control matrix $\bar{B}$ of minimal size $n \times (2n+1)$: \begin{equation*} \bar{B} = \begin{pmatrix} 1 & 1 & 0 & 0 & ... & 0 & 0 & 1/n \\ 0 & 0 & 1 & 1 & ... & 0 & 0 & 1/n \\ & & & & \ddots& & & \vdots \\ 0 & 0 & 0 & 0 & ... & 1 & 1 & 1/n \end{pmatrix}. \end{equation*} After the loss of control over one of the first $2n$ column, its undesirable effect can be completely cancelled by the identical column. The combined action of the other columns of $\bar{B}$ can then provide a net motion in any direction. Similarly, after the loss of the last column of $\bar{B}$ its effect can be overcomed by the combined action of all the others.
For a resilient system verifying $BB^\top - CC^\top \succ 0$ we derived an admissible controller \begin{equation}\label{eq:control_law} u(t) = B^\top \big( BB^\top \big)^{-1} \big( -Cw(t) + \alpha (x(t) - x_g) \big), \end{equation} with $\|u\|_{\mathcal{L}_2} \leq 1$ as long as $\|w\|_{\mathcal{L}_2} \leq 1$. For $\alpha > 0$, controller \eqref{eq:control_law} drives asymptotically the state $x$ of \eqref{eq:driftless split} to the target $x_g$.
We now return to the general linear system \eqref{eq: split}, where a control law similar to \eqref{eq:control_law} can be used if matrix $A$ is not overly unstable. The intuition is that the magnitude of $u$ in excess of $w$ can be used to counteract the instability of $A$ to a certain extent. If $BB^\top - CC^\top \succ 0$ and if $\|x_0\|$ is small enough, then there exists $\alpha > 0$ such that control law \begin{equation}\label{eq:control_law_A} u(t) := B^\top \big(BB^\top\big)^{-1} \big( -Cw(t) - \alpha x(t) \big) \end{equation} drives resilient system \eqref{eq: split} to the origin, and $\|u\|_{\mathcal{L}_2} \leq 1$ as long as $\|w\|_{\mathcal{L}_2} \leq 1$.
Now that we have solved Problem 2 for linear systems with bounded energy, let us investigate Problem 3 and the question of quantifying resilience.
Quantitative Resilience of Linear Driftless Systems (Bouvier et al., 2021) (Bouvier et al., 2024)

We want to quantify how much longer malfunctioning system \eqref{eq:driftless split} needs to reach a target $x_g \in \mathbb{R}^n$ compared to nominal system \eqref{eq:driftless}. We introduce the nominal reach time as the fastest time in which nominal system \eqref{eq:driftless} can reach target $x_g$ \begin{equation}\label{eq: T_N} T_N^*(x_g) := \underset{\bar{u}(t) \, \in \, \bar{\mathcal{U}} }{\inf} \left\{ T : x_g - x_0 = \int_0^T \hspace{-2mm} \bar{B} \bar{u}(t) dt \right\}. \end{equation} Similarly, we define the malfunctioning reach time as the fastest time in which malfunctioning system \eqref{eq:driftless split} can reach target $x_g$ when $w$ is chosen to make that time the longest \begin{equation}\label{eq: T_M} T_M^*(x_g) := \underset{w(t) \, \in \, \mathcal{W} }{\sup} \left\{ \underset{u(t) \, \in \, \mathcal{U} }{\inf} \left\{ T : x_g - x_0 = \int_0^T \hspace{-2mm} Bu(t) + Cw(t) dt \right\} \right\}. \end{equation} Then, we define the quantitative resilience of system \eqref{eq:driftless} as \begin{equation}\label{eq: r_q} r_q := \underset{x_g \, \in \, \mathbb{R}^n}{\inf} \frac{T_N^*(x_g)}{T_M^*(x_g)}. \end{equation} The larger this ratio is, the less impact the loss of control authority has on system \eqref{eq:driftless} and hence the more resilient it is. To solve Problem 3, we just need to solve optimization problem \eqref{eq: r_q}. However, the ratios of reach times are nonlinear in their dependency on targets $x_g$ making this optimization non-trivial. Additionally, our definitions of $T_N^*$ and $T_M^*$ introduce nested optimization problems rendering quantitative resilience an extremely difficult quantity to calculate.
Relying on time-optimal control theory we can simplify the expressions of the reach times $T_N^*$ and $T_M^*$. We first need to assume $rank(\bar{B}) = n$ to make system \eqref{eq:driftless} controllable. Then, using the compacity and convexity of input set $\bar{\mathcal{U}}$, theorem 4.3 of (Liberzon 2011) states that there exists a solution to \eqref{eq: T_N}. Dynamics \eqref{eq:driftless} being driftless, this time-optimal input $\bar{u}^\star$ is constant. When system \eqref{eq:driftless split} is resilient, the same reasoning applies to \eqref{eq: T_M} to obtain a constant time-optimal input $u^*(w)$ when $w$ is fixed. Proving that the worst undesirable input $w^*$ is also a constant is more technical and requires the derivation of a novel bang-bang principle. Additionally, $w^*$ is located at a vertex of polytope $\mathcal{W}$, while $u^*$ and $\bar{u}^*$ are respectively located on the boundaries of polytopes $\mathcal{U}$ and $\bar{\mathcal{U}}$. Then, optimal times $T_N^*$ and $T_M^*$ simplify to \begin{equation*} T_N^* = \underset{\bar{u} \, \in \, \bar{\mathcal{U}} }{\min} \left\{ T \geq 0 : x_g - x_0 = \bar{B} \bar{u} T \right\}, \qquad T_M^*(x_g) := \underset{w \, \in \, \mathcal{V} }{\max} \left\{ \underset{u \, \in \, \mathcal{U} }{\min} \left\{ T \geq 0 : x_g - x_0 = \big( Bu + Cw \big)T \right\} \right\}, \end{equation*} with $\mathcal{V}$ the set of vertices of $\mathcal{W}$.
We can now transform quantitative resilience into a more geometric form using polytopes $\mathcal{X} := \big\{ Cw : w \in \mathcal{W} \big\}$ and $\mathcal{Y} := \big\{ Bu : u \in \mathcal{U} \big\}$. Define the target distance $d := x_g - x_0$. Then, \begin{align*} r_q &= \underset{d \, \in \, \mathbb{R}^n_*}{\inf} \frac{T_N^*(d)}{T_M^*(d)} = \underset{d \, \in \, \mathbb{R}^n_*}{\inf} \frac{ \underset{\bar{u} \, \in \, \bar{\mathcal{U}} }{\min} \left\{ T \geq 0 : \bar{B} \bar{u} T = d \right\} }{ \underset{w \, \in \, \mathcal{V} }{\max} \left\{ \underset{u \, \in \, \mathcal{U} }{\min} \left\{ T \geq 0 : \big( Bu + Cw \big)T = d \right\} \right\} } \\ & \\ &= \underset{d \, \in \, \mathbb{R}^n_*}{\inf} \frac{ \underset{x \, \in \, \mathcal{X},\, y \, \in \, \mathcal{Y} }{\min} \left\{ T \geq 0 : (x+y) = d/T \right\} }{ \underset{x \, \in \, \mathcal{X} }{\max} \left\{ \underset{y \, \in \, \mathcal{Y} }{\min} \left\{ T \geq 0 : (x + y) = d/T \right\} \right\} } = \underset{d \, \in \, \mathbb{R}^n_*}{\inf} \frac{ \underset{x \, \in \, \mathcal{X} }{\min} \left\{ \underset{y \, \in \, \mathcal{Y} }{\max} \left\{ \alpha \geq 0 : (x + y) = \alpha d \right\} \right\} }{ \underset{x \, \in \, \mathcal{X},\, y \, \in \, \mathcal{Y} }{\max} \left\{ \alpha \geq 0 : (x+y) = \alpha d \right\} }, \end{align*} by replacing $1/T$ by $\alpha$. Since $\alpha \geq 0$, we can write $\alpha = |\alpha| = \|\alpha d\|/\|d\| = \|x+y\|/\|d\|$. Then, \begin{equation*} r_q = \underset{d \, \in \, \mathbb{S}}{\inf} \frac{ \underset{x \, \in \, \mathcal{X} }{\min} \left\{ \underset{y \, \in \, \mathcal{Y} }{\max} \left\{ \|x+y\| : x + y \in \mathbb{R}^+ d \right\} \right\} }{ \underset{x \, \in \, \mathcal{X},\, y \, \in \, \mathcal{Y} }{\max} \left\{ \|x+y\| : x+y \in \mathbb{R}^+ d \right\} }, \end{equation*} where we scaled $d$ to the unit circle $\mathbb{S}$ of $\mathbb{R}^n$. For a given direction $d$, we then need to optimize the length of vector $x+y$ knowing that it is aligned with $d$. When $C$ is a vector, i.e., when the system loses control over a single actuator, this geometrical intuition leads to the Maximax Minimax Quotient Theorem detailled in the next section. This theorem states that the direction $d$ realizing $r_q$ is aligned with vector $C$, i.e., \begin{equation*} r_q = \min \left\{ \frac{T_N^*(C)}{T_M^*(C)}, \frac{T_N^*(-C)}{T_M^*(-C)} \right\}. \end{equation*} This calculation can be even further simplified into a single linear optimization problem to determine $r_q$, while we introduced quantitative resilience as a nonlinear optimization problem with 4 nested optimizations!
The Maximax Minimax Quotient Theorem (Bouvier et al., 2022)

Let us now dive in more details about the Maximax Minimax Quotient Theorem. The problem of quantifying the resilience of driftless linear systems led us to a nonlinear optimization problem consisting of four nested optimizations : \begin{equation}\label{eq:maximax} \underset{d\, \in\, \mathbb{S}}{\max}\ r_{\mathcal{X}, \mathcal{Y}}(d) := \underset{d\, \in\, \mathbb{S}}{\max}\ \frac{\underset{x\, \in\, \mathcal{X},\ y\, \in\, \mathcal{Y}}{\max} \big\{ \|x + y\| : x + y \in \mathbb{R}^+d \big\} }{ \underset{x\, \in\, \mathcal{X}}{\min} \big\{ \underset{y\, \in\, \mathcal{Y}}{\max} \big\{ \|x + y\| : x + y \in \mathbb{R}^+d \big\} \big\} }, \end{equation} on the polytopes $\mathcal{X} := \big\{ Cw : w \in \mathcal{W} \big\}$ and $\mathcal{Y} := \big\{ Bu : u \in \mathcal{U} \big\}$.
The first step towards solving \eqref{eq:maximax} is to verify that the four optimizations all admit a solution. This is accomplished by verifying that the functions to optimize are continuous and their domain is compact. Then, in the case $\dim(\mathcal{X}) = 1$ we developed a geometrical solution to this optimization, as illustrated in the video below.
Video generated by our MATLAB code.
For optimization \eqref{eq:maximax} to make sense, we need the inclusion $\mathcal{X} \subset \mathcal{Y}$ as shown on the video. Then, we work in a 2D plane containing $\mathcal{X}$ and we parametrize direction $d$ with angle $\beta$. As $\beta$ goes from $0$ to $2\pi$, we need to find when $r_{\mathcal{X}, \mathcal{Y}}(\beta)$ reaches its maximum. On the video, the two parts of the red broken arrow represent the $x$ and $y$ solutions of the numerator of \eqref{eq:maximax} as they maximize the length $\|x+y\|$ while being aligned with $d$. Similarly, the two parts of the blue broken arrow represent the $x$ and $y$ solutions of the denominator of \eqref{eq:maximax} as this $x$ is picked to minimize $\|x+y\|$, while $y$ aims at maximizing it and aligning it with $d$.
Notice that in the video, when both broken arrows intersect the same face of $\mathcal{Y}$, ratio $r_{\mathcal{X}, \mathcal{Y}}$ is constant. It only changes value at vertex crossings. Using simple trigonometry, it is possible to differentiate the vertices where the value of $r_{\mathcal{X}, \mathcal{Y}}$ increases or decreases. Then, it becomes clear that the maximum of $r_{\mathcal{X}, \mathcal{Y}}$ occurs when both $d$ is aligned with $\mathcal{X}$. Since this holds for any 2D plane containing $\mathcal{X}$, the maximum over all $d \in \mathbb{S}$ also occurs along $\mathcal{X}$, which concludes the proof.
We will now investigate how to extend resilience theory to non-driftless linear systems with inputs of bounded amplitude.
Resilience of Linear Systems (Bouvier et al., 2022) (Bouvier et al., 2023)

We now return to the initial non-driftless dynamics \eqref{eq: ODE} and \eqref{eq: split} but the input sets $\bar{\mathcal{U}}$, $\mathcal{U}$ and $\mathcal{W}$ are now polytopes instead of relying on $\mathcal{L}_2$-bounds. To establish resilience conditions for these systems in a more understandable form than \eqref{eq:thm2}, we build on the differential games theory of (Hájek 1974). This duality result states the equivalence between the resilient stabilizability of \eqref{eq: split} and the stabilizability of system \begin{equation}\label{eq: Hajek} \dot x(t) = Ax(t) + z(t), \qquad x(0) = x_0 \in \mathbb{R}^n, \quad z(t) \in \mathcal{Z}, \end{equation} where $\mathcal{Z} \subset \mathbb{R}^n$ is the Minkowski difference between the set of admissible control inputs $B\mathcal{U} := \big\{Bu : u \in \mathcal{U} \big\}$, and the opposite of the set of undesirable inputs $C\mathcal{W} := \big\{Cw : w \in \mathcal{W} \big\}$, i.e., \begin{equation*} \mathcal{Z} := B\mathcal{U} \ominus (−C\mathcal{W}) = \big\{ z \in B\mathcal{U} : z − Cw \in B\mathcal{U}\ \text{for all}\ w \in \mathcal{W} \big\}. \end{equation*} Set $\mathcal{Z}$ represents the control authority left after counteracting the worst possible undesirable inputs $Cw$. System \eqref{eq: split} is resiliently stabilizable if for all $x_0 \in \mathbb{R}^n$ and all $w(\cdot) \in \mathcal{W}$, there exists $T \geq 0$ and a control $u(\cdot) \in \mathcal{U}$ driving the state of \eqref{eq: split} from $x_0$ to $x(T) = 0$. System \eqref{eq: Hajek} is stabilizable if for all $x_0 \in \mathbb{R}^n$, there exists $T \geq 0$ and a control $z(\cdot) \in \mathcal{Z}$ driving the state of \eqref{eq: Hajek} from $x_0$ to $x(T) = 0$.
Let $q := dim(\mathcal{Z})$ and define a matrix $Z \in \mathbb{R}^{n \times q}$ such that $Im(Z) = span(\mathcal{Z})$. Then, we can formulate a resilient stabilizability condition by building on the stabilizability condition of (Brammer 1972). System \eqref{eq: split} is resiliently stabilizable if and only if $rank \big(\mathcal{C}(A,Z)\big) = n$, $Re\big( \lambda(A) \big) \leq 0$, and there is no real eigenvector $v$ of $A^\top$ satisfying $v^\top z \leq 0$ for all $z \in \mathcal{Z}$.
To quantify the resilience of linear systems, we reuse the nominal reach time $T_N^*$ and the malfunctioning reach time $T_M^*$. However, the dynamics being non-driftless, these reach times now depend on both the initial state $x_0$ and the target $x_g$, not just their difference $d$. These modifications appear in the nominal reach time \begin{equation}\label{eq: T_N non-drift} T_N^*(x_0, x_g) := \underset{\bar{u}(t) \, \in \, \bar{\mathcal{U}} }{\inf} \left\{ T \geq 0 : x_g = e^{AT}\left( x_0 + \int_0^T \hspace{-2mm} e^{-At}\bar{B} \bar{u}(t) dt\right) \right\}, \end{equation} the malfunctioning reach time \begin{equation}\label{eq: T_M non-drift} T_M^*(x_0, x_g) := \underset{w(t) \, \in \, \mathcal{W} }{\sup} \left\{ \underset{u(t) \, \in \, \mathcal{U} }{\inf} \left\{ T \geq 0 : x_g = e^{AT}\left( x_0 + \int_0^T \hspace{-2mm} e^{-At}\big(Bu(t) + Cw(t) \big)dt \right)\right\} \right\}, \end{equation} and the quantitative resilience $$r_q := \underset{x_0 \, \in \, \mathbb{R}^n, \ x_g \, \in \, \mathbb{R}^n}{\inf} \frac{T_N^*(x_0, x_g)}{T_M^*(x_0, x_g)}.$$
Because dynamics \eqref{eq: ODE} and \eqref{eq: split} are not driftless, the arguments of the solutions of \eqref{eq: T_N non-drift} and \eqref{eq: T_M non-drift} are time-varying bang-bang signals and not constants anymore. Therefore, none of the geometrical work developed previously can be reused to calculate $T_N^*$ and $T_M^*$, only algorithmical solutions exist. Instead, relying on Lyapunov theory we derived analytical bounds on $T_N^*$, $T_M^*$ and $r_q$. Assuming that $A$ is Hurwitz, there exists $P \succ 0$ and $Q \succ 0$ such that $A^\top P + PA = -Q$, which also defines a $P$-norm as $\|x\|_P := \sqrt{x^\top P x}$. Further assuming the stabilizability of nominal system \eqref{eq: ODE} yields \begin{equation*} 2 \frac{\lambda^P_{min}}{\lambda^Q_{max}} ln \left(1 + \frac{\lambda^Q_{max} \|x_0\|_P}{2 \lambda^P_{min} b^P_{max}}\right) \leq T_N^*(x_0) \leq 2 \frac{\lambda^P_{max}}{\lambda^Q_{min}} ln \left(1 + \frac{\lambda^Q_{min} \|x_0\|_P}{2 \lambda^P_{max} b^P_{min}}\right), \end{equation*} with $b^P_{max} := \max \big\{ \| \bar{B} \bar{u} \|_P : \bar{u} \in \bar{\mathcal{U}} \big\}$ and $b^P_{min} := \min \big\{ \| \bar{B} \bar{u} \|_P : \bar{u} \in \partial \bar{\mathcal{U}} \big\}$. Malfunctioning reach time $T_M^*$ can be bounded similarly \begin{equation*} 2 \frac{\lambda^P_{min}}{\lambda^Q_{max}} ln \left(1 + \frac{\lambda^Q_{max} \|x_0\|_P}{2 \lambda^P_{min} z^P_{max}}\right) \leq T_M^*(x_0) \leq 2 \frac{\lambda^P_{max}}{\lambda^Q_{min}} ln \left(1 + \frac{\lambda^Q_{min} \|x_0\|_P}{2 \lambda^P_{max} z^P_{min}}\right), \end{equation*} with $z^P_{max} := \max \big\{ \| z \|_P : z \in \mathcal{Z} \big\}$ and $z^P_{min} := \min \big\{ \| z \|_P : z \in \partial \mathcal{Z} \big\}$. Combining their bounds allows to estimate quantitative resilience analytically \begin{equation*} \max \left( \frac{\lambda^P_{min} \lambda^Q_{min}}{\lambda^P_{max} \lambda^Q_{max}}, \frac{z^P_{min}}{b^P_{max}}\right) \leq r_q \leq \max \left( \frac{\lambda^P_{max} \lambda^Q_{max}}{\lambda^P_{min} \lambda^Q_{min}}, \frac{z^P_{max}}{b^P_{min}}\right). \end{equation*}
We have now addressed all three problems of interest for linear systems with different types of input bounds. Let us see if we can extend the scope of resilience theory by removing a few of its limitations.
Resilience of an Orbital Inspection Mission (Bouvier et al., 2023)

In this section we demonstrate the resilience of a spacecraft to perform an orbital inspection mission depsite the loss of control authority over one of its thrusters. To make our application more realistic, we consider the controller to be further plagued by actuation delay, hence preventing it from instantaneously cancelling undesirable inputs. Then, this application scenario requires an extension of resilience theory to three new settings:
- resilience despite actuation delay;
- resilient trajectory tracking;
- resilience of nonlinear systems.
A major limitation of resilience theory is the requirement that the controller $u(t)$ has immediate knowledge of the undesirable inputs $w(t)$. To account for more realism, we add a constant actuation delay $\tau > 0$ to the controller. Then, the controller knowledge at time $t > \tau$ can be written as $u(t) = u\big(t, x[0:t-\tau], w[0:t-\tau]\big)$. Aware of this delay, the controller can use a state predictor to improve its accuracy (Léchappé 2015).
The satellite under study is tasked with performing an orbital inspection of another satellite. To do so, it follows a fuel-optimal trajectory linking four waypoints where it will take a picture of the target satellite as shown below.
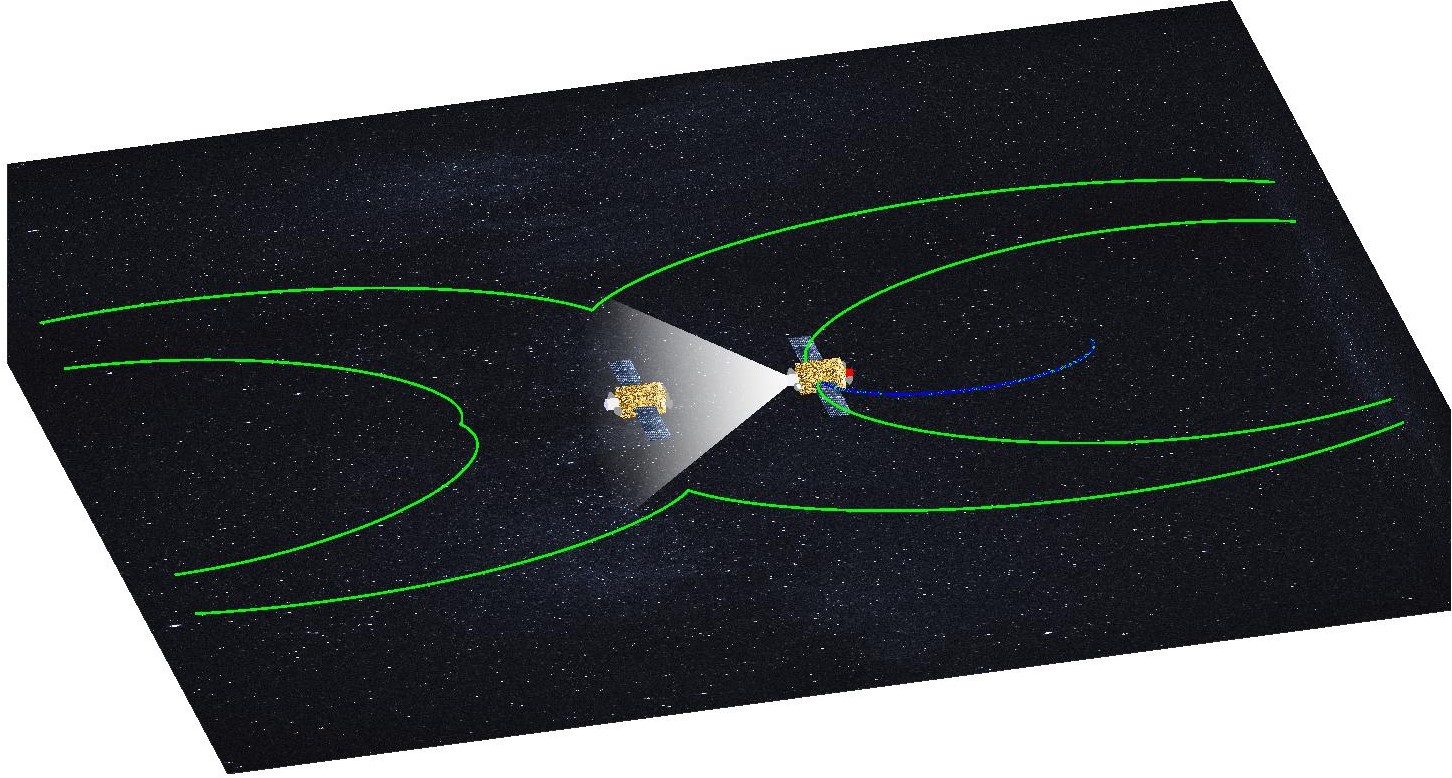
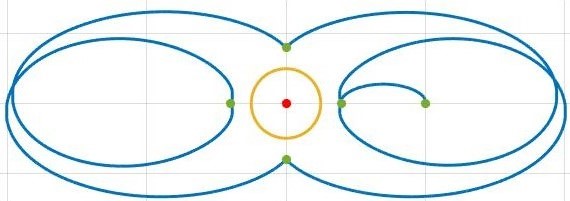
to inspect the target satellite (red) without breaching the Keep-Out Sphere (yellow).
Since the inspecting satellite must always point at its target, the satellite is actually rotating along its trajectory. To handle this nonlinearity, we partially extended resilience theory to nonlinear systems by building from (Hájek 1974)'s framework.

The undesirable thrust is shown in red, while the controlled thrust is cyan.
The reference trajectory is in green, while the actual path of the satellite is shown in blue.
Video generated by our Matlab code.
Quick Summary
- A loss of control authority over actuators is characterized by actuators producing uncontrolled and possibly undesirable outputs within their full range.
- An autonomous system is resilient to such a malfunction if for any undesirable input $w$ there exists a control $u$ driving the state to its target.
- We can assess analytically whether a linear system is resilient or not and we know how to design resilient systems.
- We can quantify the resilience of linear systems by comparing nominal and malfunctioning reach times.
References
-
M. Bartels, "Russia says ’software failure’ caused thruster misfire at space station", space.com, 2021.
-
H. Fawzi, P. Tabuada, and S. Diggavi, "Secure estimation and control for cyber-physical systems under adversarial attacks", IEEE Transactions on Automatic Control, vol. 59, no. 6, pp. 1454–1467, 2014.
-
A. A. Amin and K. M. Hasan, "A review of fault tolerant control systems: Advancements and applications", Measurement, vol. 143, pp. 58–68, 2019.
-
L. Y. Wang and J.-F. Zhang, "Fundamental limitations and differences of robust and adaptive control", in 2001 American Control Conference, vol. 6, pp. 4802–4807, 2001.
-
J.-B. Bouvier and M. Ornik, "Resilient reachability for linear systems", in 21st IFAC World Congress, 2020, pp. 4409–4414.
-
M. Delfour and S. Mitter, "Reachability of perturbed systems and min sup problems", SIAM Journal on Control and Optimization, vol. 7, no. 4, pp. 521–533, 1969.
-
J.-B. Bouvier and M. Ornik, "Designing resilient linear systems", IEEE Transactions on Automatic Control, vol. 67, no. 9, pp. 4832–4837, 2022.
-
J.-B. Bouvier, K. Xu, and M. Ornik, "Quantitative resilience of linear driftless systems", in SIAM Conference on Control and its Applications, 2021, pp. 32–39.
-
J.-B. Bouvier, K. Xu, and M. Ornik, "Quantitative resilience of generalized integrators", IEEE Transactions on Automatic Control, 2024.
-
D. Liberzon, "Calculus of Variations and Optimal Control Theory: a Concise Introduction", Princeton University Press, 2011.
-
J.-B. Bouvier and M. Ornik, "The Maximax Minimax Quotient Theorem", Journal of Optimization Theory and Applications, vol. 192, pp. 1084–1101, 2022.
-
J.-B. Bouvier and M. Ornik, "Quantitative resilience of linear systems", in 20th European Control Conference, 2022, pp. 485–490.
-
J.-B. Bouvier and M. Ornik, "Resilience of linear systems to partial loss of control authority", Automatica, vol. 152, 2023.
-
O. Hájek, "Duality for differential games and optimal control", Mathematical Systems Theory, vol. 8, no. 1, pp. 1–7, 1974.
-
R. Brammer, "Controllability in linear autonomous systems with positive controllers", SIAM Journal on Control, vol. 10, no. 2, pp. 339–353, 1972.
-
J.-B. Bouvier, H. Panag, R. Woollands, and M. Ornik, "Resilient trajectory tracking to partial loss of control authority over actuators with actuation delay", ArXiv, 2023.
-
V. Léchappé, E. Moulay, F. Plestan, A. Glumineau, and A. Chriette, "New predictive scheme for the control of LTI systems with input delay and unknown disturbances", Automatica, vol. 52, pp. 179–184, 2015.