Safety in Reinforcement Learning

April 30, 2024 | min | Jean-Baptiste Bouvier

Safety in Reinforcement Learning (RL) typically consists in enforcing a constraint to prevent trajectories from entering some unsafe region. We are interested in closed-loop constrained RL, where the constraint on the state of the system is enforced by a learned policy, as illustrated below.

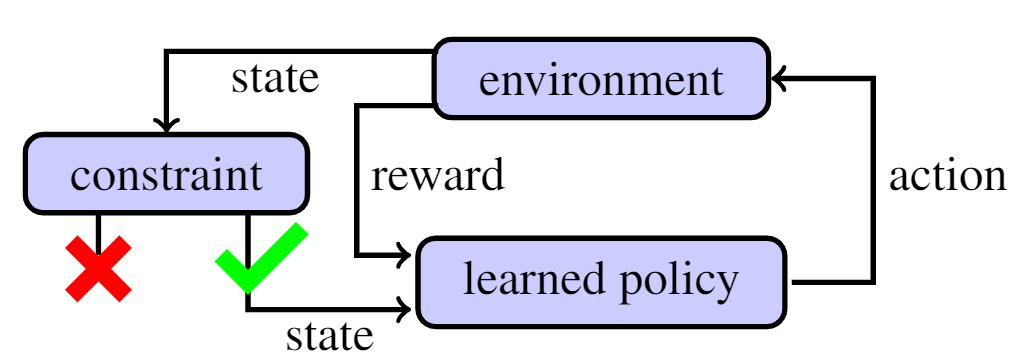
The learned policy predicts an action to be taken. This action modifies the state of the environment environment and produces a reward signal. The policy learns to maximize this reward by improving its action prediction at any given state. In this post we will review how constraints are implemented in safe RL.

Framework

Following the review work of Brunke et al. 2022, we distinguish three safety levels used in RL depending on the type of constraint employed. The lowest level of safety is provided by soft constraints, which only encourage the policy to respect the constraint through reward shaping, but no guarantees are provided. The intermediate safety level is obtained with probabilistic constraints, which provide an upper bound to the probability of violating the constraint. Finally, the highest level of safety is enforced by hard constraints, which guarantee no constraint violations. These three safety levels are illustrated below.

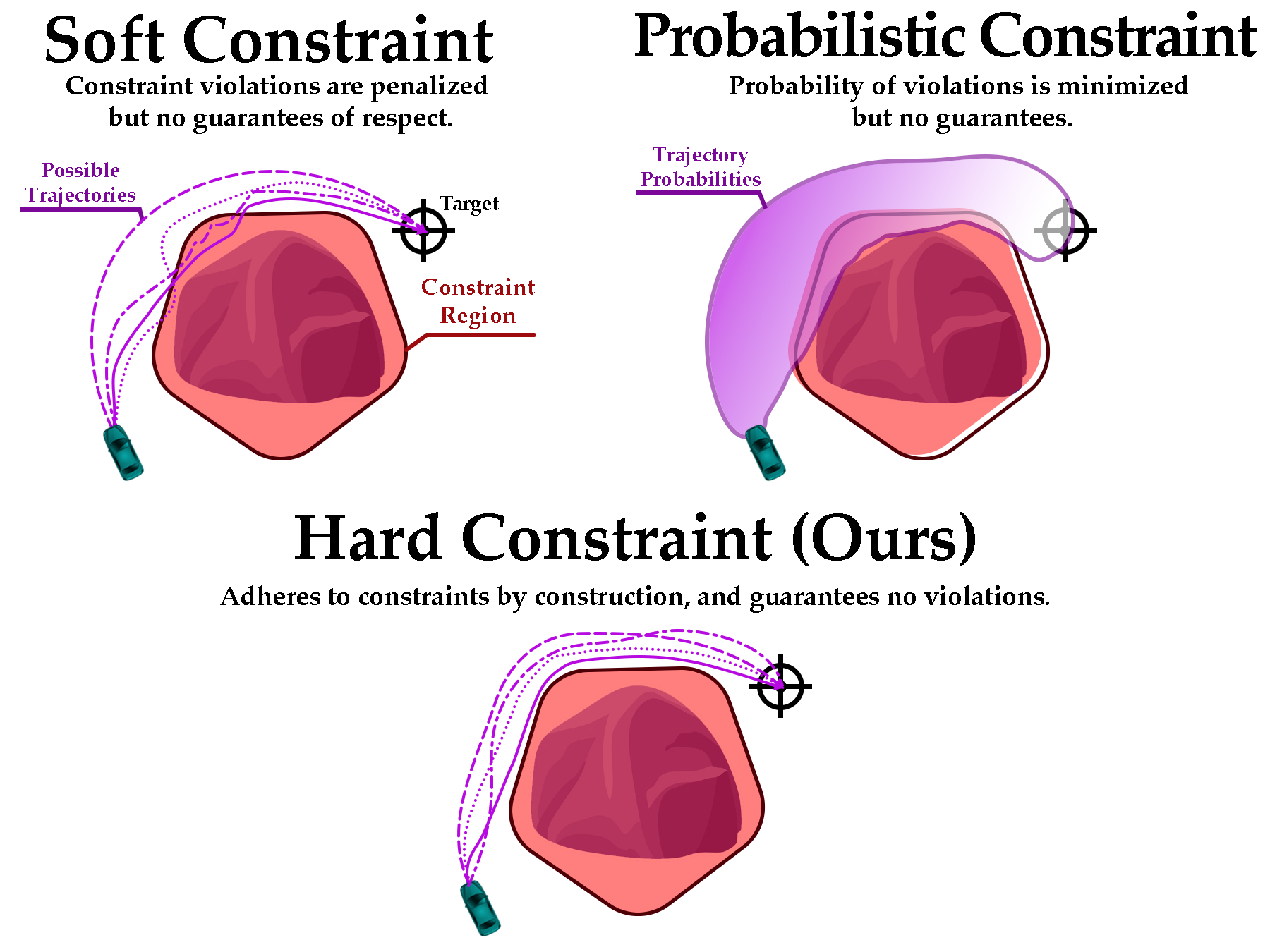
We will now discuss in greater detail these three levels of safety and their corresponding type of constraint.

Soft Constraints

The most common approach to enforce constraints in RL adopts the framework of constrained Markov decision processes (CMDPs) (Altman 2021). CMDPs encourage policies to respect constraints by penalizing the expectation of the cumulative constraint violations (Liu et al. 2023).

Numerous variations of this framework have been developed such as state-wise constrained MDP (Zhao et al. 2023), constrained policy optimization (Achiam et al. 2017), and state-wise constrained policy optimization (Zhao et al. 2023). These approaches belong to the category of soft constraints as the policy is only encouraged to respect the constraint and provides no satisfaction guarantees. This category also encompasses work (Meng et al. 2023) where a control barrier transformer is trained to avoid unsafe actions, but no safety guarantees can be derived.

Probabilisitic Constraints

A probabilistic constraint comes with the guarantee of satisfaction with some probability threshold (Brunke et al. 2022) and hence ensures a higher level of safety than soft constraints. For instance, (Kalagarla et al. 2021) derived policies having a high probability of not violating the constraints by more than a small tolerance. Using control barrier functions, (Cheng et al. 2019) guaranteed safe learning with high probability.

Since unknown stochastic environments prevent hard constraints enforcement, (Wang et al. 2023) proposed to learn generative model-based soft barrier functions to encode chance constraints. Similarly, by using a safety index on an unknown environment modeled by Gaussian processes, (Zhao et al. 2023), (Knuth et al. 2021) established probabilistic safety guarantees.

Hard Constraints

The third and highest safety level corresponds to inviolable hard constraints (Brunke et al. 2022). Work (Pham et al. 2018) learns a safe policy thanks to a differentiable safety layer projecting any unsafe action onto the closest safe action. However, since this safety layers only correct actions, a precise model of the robot dynamics model must be known, which is typically unavailable in RL settings. This limitation is also shared by (Rober et al. 2023), which requires knowledge of the robot dynamics model to compute its backward reachable sets and avoid obstacles.

To circumvent any knowledge of the robot dynamics model, (Zhao et al. 2022) used an implicit black-box model of the environment but is restricted to collision avoidance problems in 2D. To avoid this limitations, the Lagrangian-based approach of (Ma et al. 2022) and the model-free approach of (Yang et al. 2023) both learn a safety certificate with a deep neural network. However, to ensure that these neural net approximators actually verify the safety guarantees of their analytical counterparts, they would need to be evaluated at every point of their state space, which is infeasible in practice. Hence, the safety guarantees of these approaches only hold for the states where their neural networks verify the safety certificate equations.

This lack of provable constraint satisfaction prompted our work POLICEd RL where we establish an algorithm to enforce an affine hard constraint on a learned policy in closed-loop with a black-box deterministic environment (Bouvier et al. 2024).

Quick Summary

• Safe RL works can be grouped together based on the type of constraints they consider, which lead to one of three safety level.
• The lowest level of safety is provided by soft constraints, which only encourage the policy to respect the constraint through reward shaping, but no guarantees are provided.
• The intermediate safety level is obtained with probabilistic constraints, which provide an upper bound to the probability of violating the constraint.
• Finally, the highest level of safety is enforced by hard constraints, which guarantee no constraint violations.

References

1. Joshua Achiam, David Held, Aviv Tamar, and Pieter Abbeel, Constrained Policy Optimization, International Conference on Machine Learning, pages 22 – 31. PMLR, 2017.
2. Eitan Altman, Constrained Markov Decision Processes, Routledge, 2021.
3. Jean-Baptiste Bouvier, Kartik Nagpal, and Negar Mehr, POLICEd RL: Learning Closed-Loop Robot Control Policies with Provable Satisfaction of Hard Constraints, 2024.
4. Lukas Brunke, Melissa Greeff, Adam W Hall, Zhaocong Yuan, Siqi Zhou, Jacopo Panerati, and Angela P Schoellig, Safe learning in robotics: From learning-based control to safe reinforcement learning, Annual Review of Control, Robotics, and Autonomous Systems, 5:411 – 444, 2022.
5. Richard Cheng, Gábor Orosz, Richard M Murray, and Joel W Burdick, End-to-end safe reinforcement learning through barrier functions for safety-critical continuous control tasks, Proceedings of the AAAI Conference on Artificial Intelligence, volume 33, pages 3387–3395, 2019.
6. Krishna C Kalagarla, Rahul Jain, and Pierluigi Nuzzo, A sample-efficient algorithm for episodic finite-horizon MDP with constraints, Proceedings of the AAAI Conference on Artificial Intelligence, volume 35, pages 8030–8037, 2021.
7. Craig Knuth, Glen Chou, Necmiye Ozay, and Dmitry Berenson, Planning with learned dynamics: Probabilistic guarantees on safety and reachability via Lipschitz constants, IEEE Robotics and Automation Letters, 6(3):5129–5136, 2021.
8. Zuxin Liu, Zijian Guo, Yihang Yao, Zhepeng Cen, Wenhao Yu, Tingnan Zhang, and Ding Zhao, Constrained Decision Transformer for Offline Safe Reinforcement Learning, arXiv preprint arXiv:2302.07351, 2023.
9. Haitong Ma, Jianyu Chen, Shengbo Eben, Ziyu Lin, Yang Guan, Yangang Ren, and Sifa Zheng, Model-based Constrained Reinforcement Learning using Generalized Control Barrier Function, IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pages 4552–4559. IEEE, 2021.
10. Haitong Ma, Changliu Liu, Shengbo Eben Li, Sifa Zheng, and Jianyu Chen, Joint Synthesis of Safety Certificate and Safe Control Policy using Constrained Reinforcement Learning, Learning for Dynamics and Control Conference, pages 97–109. PMLR, 2022.
11. Yue Meng, Sai Vemprala, Rogerio Bonatti, Chuchu Fan, and Ashish Kapoor, ConBaT: Control Barrier Transformer for Safe Policy Learning, arXiv preprint arXiv:2303.04212, 2023.
12. Tu-Hoa Pham, Giovanni De Magistris, and Ryuki Tachibana, OptLayer: Practical Constrained Optimization for Deep Reinforcement Learning in the Real World, International Conference on Robotics and Automation (ICRA), pages 6236–6243. IEEE, 2018.
13. Nicholas Rober, Sydney M Katz, Chelsea Sidrane, Esen Yel, Michael Everett, Mykel J Kochenderfer, and Jonathan P How, Backward reachability analysis of neural feedback loops: Techniques for linear and nonlinear systems, IEEE Open Journal of Control Systems, 2:108–124, 2023.
14. Yixuan Wang, Simon Sinong Zhan, Ruochen Jiao, Zhilu Wang, Wanxin Jin, Zhuoran Yang, Zhaoran Wang, Chao Huang, and Qi Zhu, Enforcing hard constraints with soft barriers: Safe reinforcement learning in unknown stochastic environments, International Conference on Machine Learning, pages 36593–36604. PMLR, 2023.
15. Yujie Yang, Yuxuan Jiang, Yichen Liu, Jianyu Chen, and Shengbo Eben Li, Model-free safe reinforcement learning through neural barrier certificate, IEEE Robotics and Automation Letters, 8(3):1295–1302, 2023.
16. Weiye Zhao, Tairan He, and Changliu Liu, Model-free safe control for zero-violation reinforcement learning, 5th Annual Conference on Robot Learning, pages 784–793. PMLR, 2022.
17. Weiye Zhao, Rui Chen, Yifan Sun, Tianhao Wei, and Changliu Liu, State-wise Constrained Policy Optimization, arXiv preprint arXiv:2306.12594, 2023.
18. Weiye Zhao, Tairan He, and Changliu Liu, Probabilistic Safeguard for Reinforcement Learning using Safety Index Guided Gaussian Process Models, Learning for Dynamics and Control Conference, pages 783–796. PMLR, 2023.
19. Weiye Zhao, Yifan Sun, Feihan Li, Rui Chen, Tianhao Wei, and Changliu Liu, Learn with imagination: Safe set guided state-wise constrained policy optimization, arXiv preprint arXiv:2308.13140, 2023.