An Overview of "POLICEd RL: Learning Closed-Loop Robot Control Policies with Provable Satisfaction of Hard Constraints"
June 4, 2024 | min | Jean-Baptiste Bouvier
In this post I will introduce the work I completed with Kartik Nagpal and Prof. Negar Mehr. I presented this work at the 2024 Robotics: Science and Systems (RSS) conference. The full paper is available on ArXiv.
Introduction
As discussed in my previous post, safety in reinforcement learning (RL) is typically not guaranteed, but only encouraged through reward shaping. Provable guarantees of hard constraint satisfaction are much more difficult to obtain. Indeed, previous attempts typically suffer from one of these two limitations: either they need an accurate model of the environment, or their learned 'safety certificate' only approximates without guarantees an actual safety certificate. On the other hand, our POLICEd RL approach can provably enforce hard constraint satisfaction in closed-loop with a black-box environment.
Framework
Consider a robot of state $s \in \mathcal{S}$ with black-box dynamics \begin{equation}\label{eq: nonlinear dynamics} \dot s(t) = f\big( s(t), a(t) \big), \end{equation} where $a(t) \in \mathcal{A}$ denotes an admissible action. The state of the robot is constrained by a single affine inequality \begin{equation}\label{eq: constraint} C s(t) \leq d, \quad \text{for all}\ t \geq 0. \end{equation} The action is chosen by a deterministic feedback policy $a(t) = \mu_\theta\big( s(t) \big) \in \mathcal{A}$ modeled by a deep neural network $\mu_\theta$ parameterized by $\theta$. Applying this policy in environment \eqref{eq: nonlinear dynamics} generates a reward signal $R\big( s(t), a(t)\big)$, as illustrated below.
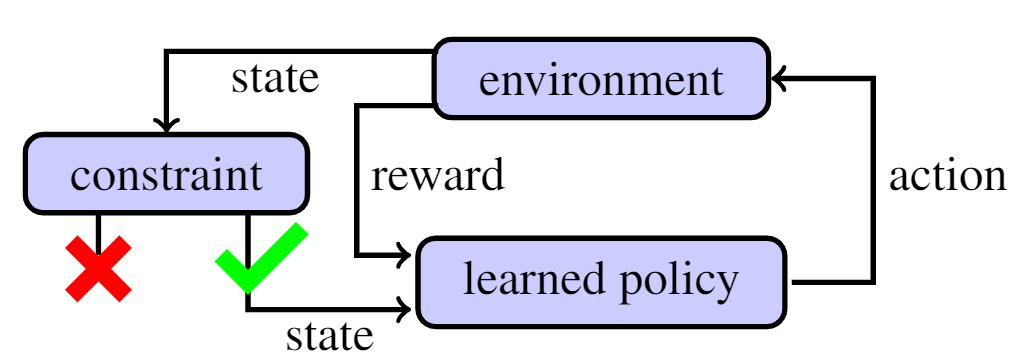
Our objective is to train $\mu_\theta$ to maximize the expected discounted reward while respecting constraint \eqref{eq: constraint} at all times, i.e., \begin{equation}\label{eq: expected reward} \underset{\theta}{\max}\, \mathcal{G}(\mu_\theta) := \underset{s(0)}{\mathbb{E}} \int_0^{\infty} \hspace{-2mm} \gamma^t R\big( s(t), \mu_\theta(s(t))\big) dt \hspace{2mm} \text{s.t.}\ \eqref{eq: constraint}, \end{equation} where $\gamma \in (0,1)$ is a discount factor. We emphasize that constraint \eqref{eq: constraint} is a hard constraint to be respected at all times.
Preliminaries
We build our approach on the POLICE algorithm (Balestriero and LeCun 2023) which uses the spline theory of neural networks (Balestriero and Baraniuk 2018) to modify their training to make their outputs strictly affine within a user-specified region as shown below.
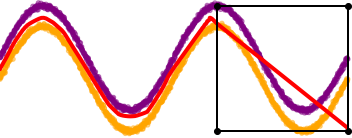
POLICE (Balestriero and LeCun 2023) guarantees the deep neural network is affine in the region of interest.
Image from (Bouvier et al. 2024).
Constrained Reinforcement Learning
To enforce the satisfaction of affine constraint $Cs \leq d$, we will construct a buffer region $\mathcal{B}$ encompassing all states $s$ judged too close from the constraint line $Cs = d$, as illustrated in the image below. We will make this region repulsive by enforcing $C\dot s \leq 0$ for all $s \in \mathcal{B}$. This will then guarantee that closed-loop trajectories of the robot cannot breach the constraint.
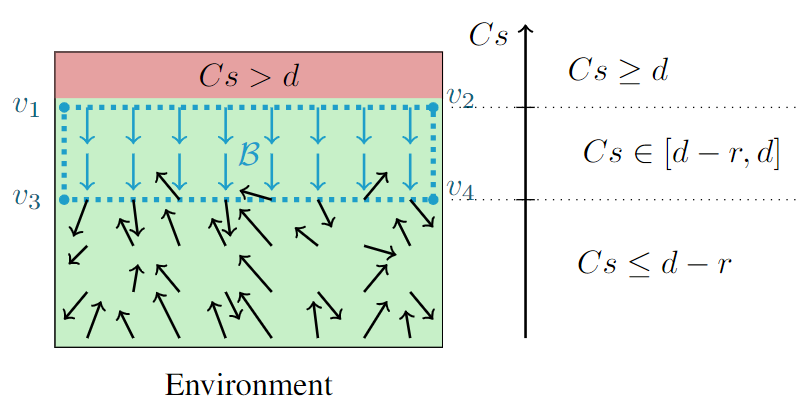
We start by constructing this buffer region of 'radius' $r > 0$, defined as \begin{equation}\label{eq: buffer} \mathcal{B} := \big\{ s \in \mathcal{S} : C s \in [d - r, d]\big\}. \end{equation} Note that any state trajectory initially verifying constraint \eqref{eq: constraint}, i.e., $Cs(0) \leq d$, has to cross buffer $\mathcal{B}$ before being able to violate the constraint. Therefore, if buffer $\mathcal{B}$ cannot be crossed, constraint \eqref{eq: constraint} cannot be violated.
We choose a deterministic policy $\mu_\theta : \mathcal{S} \rightarrow \mathcal{A}$ modeled by a deep neural network with ReLU activations and linear layers implementing the POLICE algorithm (Balestriero and LeCun 2023). This algorithm allows to enforce $\mu_\theta$ to be affine over polytopic region $\mathcal{B}$. Thus, there exists constant matrices $D_{\theta}$ and $e_{\theta}$ such that \begin{equation}\label{eq: police} \mu_\theta(s) = D_{\theta} s + e_{\theta} \quad \text{for all}\ s \in \mathcal{B}. \end{equation} Training policy $\mu_\theta$ with any RL algorithm will optimize the values of $D_\theta$, $e_\theta$, and $\mu_\theta$ outside of $\mathcal{B}$ to maximize \eqref{eq: expected reward}. The POLICE algorithm (Balestriero and LeCun 2023) only enforces the affine structure of $\mu_\theta$ over $\mathcal{B}$, not the specific values of $D_{\theta}$ and $e_{\theta}$.
To simplify the constraint enforcement process, we would like the dynamics to be affine. However, in general, robot dynamics \eqref{eq: nonlinear dynamics} are nonlinear. We will thus use an affine approximation of \eqref{eq: nonlinear dynamics} inside buffer $\mathcal{B}$ with the following definition.
Definition. An approximation measure $\varepsilon$ of dynamics \eqref{eq: nonlinear dynamics} with respect to constraint \eqref{eq: constraint} and buffer \eqref{eq: buffer} is any $\varepsilon \geq 0$ for which there exists constant matrices $A$, $B$, and $c$ such that \begin{equation}\label{eq: approximation} \big| C f(s, a) - C(A s + B a + c) \big| \leq \varepsilon, \end{equation} for all $s \in \mathcal{B}$, and all $a \in \mathcal{A}$.
Intuitively, the value of $\varepsilon$ quantifies how far from affine are dynamics \eqref{eq: nonlinear dynamics} over buffer $\mathcal{B}$. We can use data-driven techniques to estimate $\varepsilon$. Then, we can show how to guarantee satisfaction of constraint \eqref{eq: constraint} by black-box environment \eqref{eq: nonlinear dynamics} armed only with an approximation measure $\varepsilon$ and without knowing matrices $A$, $B$, $c$ or dynamics $f$.
Theorem 1. For any approximation measure $\varepsilon$, if at each vertex $v$ of buffer $\mathcal{B}$ repulsion condition \begin{equation}\label{eq: repulsion} Cf\big(v, \mu_\theta(v) \big) \leq -2\varepsilon, \end{equation} holds, then $Cs(0) < d$ yields $Cs(t) < d$ for all $t \geq 0$.
Proof: The intuition behind this proof is to use \eqref{eq: repulsion} and approximation \eqref{eq: approximation} to show that $C\dot s \leq 0$ for all $s \in \mathcal{B}$, which in turn prevents trajectory from crossing buffer $\mathcal{B}$ and hence from violating the constraint. Full proof available in (Bouvier et al. 2024).
Theorem 1 guarantees that trajectories steered by $\mu_\theta\big( s(t) \big)$ satisfy constraint \eqref{eq: constraint} at all times as long as repulsion condition \eqref{eq: repulsion} is satisfied. This is the major strength of POLICEd RL: to ensure constraint satisfaction we only need to check whether \eqref{eq: repulsion} holds at the vertices of $\mathcal{B}$. Without POLICE, $\mu_\theta$ would not be affine over $\mathcal{B}$, and repulsion condition \eqref{eq: repulsion} would need to be verified at all states $s \in \mathcal{B}$.
Simulations
2D system
We first illustrate POLICEd RL on a simple 2D example where the agent must learn to reach a target while avoiding an obstacle. The arrows in the affine buffer shows whether the agent learns to go around the obstacle.
The affine policy in buffer $\mathcal{B}$ (green) pushes states away from the constraint line (red) before heading towards the target (cyan).
Inverted pendulum experiment
We test POLICEd RL on the inverted pendulum environment with the MuJoCo physics engine. To maintain the pendulum upright and prevent it from falling past $\theta_{max} = 0.2\, rad$, we aim at enforcing constraint $\dot \theta(t) \leq 0$ for $\theta(t) \in [0.1, 0.2]\, rad$.
We use Proximal Policy Optimization (PPO) (Schulman et al. 2017) to learn both a baseline and a POLICEd policy. The baseline is a standard PPO policy that does not have the enforced affine buffer $\mathcal{B}$ of the POLICEd policy. They both follow the same training procedure in the same environment where they receive identical penalties for constraint violations. The reward curves below show that both methods achieve maximal reward.
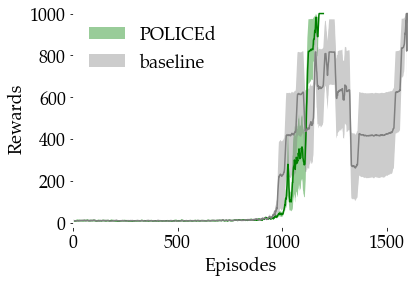
The solid lines correspond to the average and the shaded regions to the 95% confidence interval over 5 runs.
Image from (Bouvier et al. 2024).
During training we measure the proportion of buffer $\mathcal{B}$ where repulsion condition $C\dot s \leq -2\varepsilon$ is satisfied and report these proportions below. Since the POLICEd policy achieves maximal reward while completely satisfying repulsion condition \eqref{eq: repulsion} at episode 1180 it stops training. However, the figure below shows that the baseline never succeeds in enforcing $C\dot s \leq -2\varepsilon$ over the entire buffer. Moreover, trying to improve constraint satisfaction causes a large drop in the baseline rewards as seen after episode 1300. Our POLICEd policy guarantees the satisfaction of constraint $\dot\theta \leq 0$ by enforcing repulsion condition \eqref{eq: repulsion}, i.e., $\ddot \theta \leq 0$. Consequently, it guarantees that trajectories starting from $\dot \theta(0) < 0$ will never reach any state where $\dot \theta(t) \geq 0$.
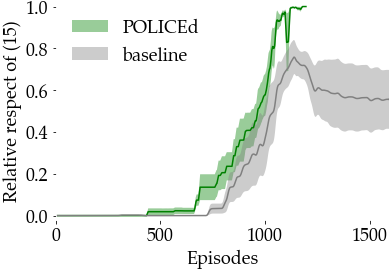
The baseline never succeeds in entirely enforcing \eqref{eq: repulsion} hence allowing possible constraint violations.
The solid lines correspond to the average and the shaded regions to the 95% confidence interval over 5 runs.
Image from (Bouvier et al. 2024).
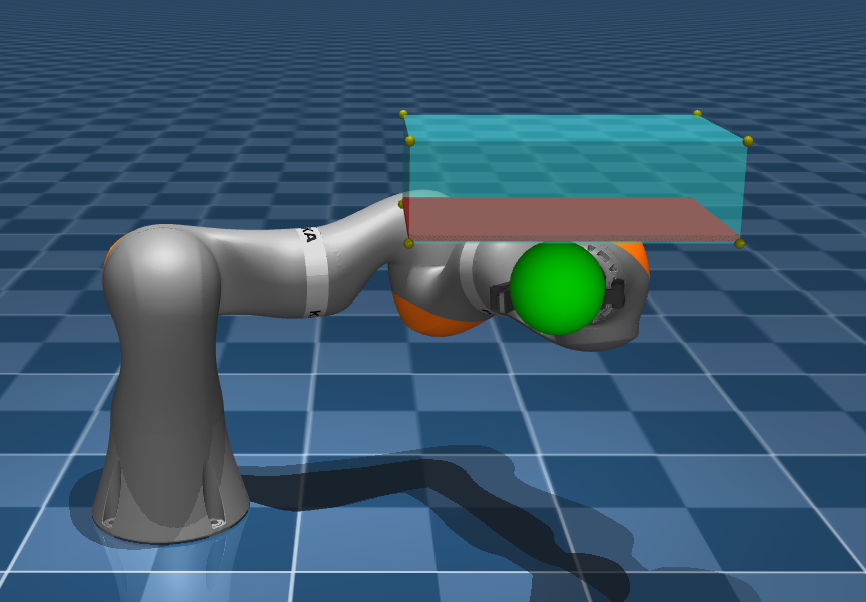
Robotic arm
We further showcase our method on a KUKA robotic arm with 7 degrees of freedom implemented in the high-fidelity MuJoCo simulator. The goal is to reach a target while avoiding an unsafe region as illustrated below.
The POLICEd method uses a buffer region (cyan).
Images from (Bouvier et al. 2024).
We learn a baseline and a POLICEd policy using Twin Delayed DDPG (TD3) (Fujimoto et al. 2018), an improved version of Deep Deterministic Policy Gradient (DDPG). While we believe ours is the first paper to provably enforce hard constraints with black-box environments, safe RL has produced remarkable works in soft constraints and learned safety certificate methods. As such, we also compare our approach with the soft constraint method Constrained Policy Optimization (CPO) (Achiam et al. 2017), as well as the learned control barrier function approach PPO-Barrier of (Yang et al. 2023).
After training all these models, we deploy them for 500 episodes on the safe arm task. From these episodes we collected a series of metrics summarizing their performance and their constraint respect.
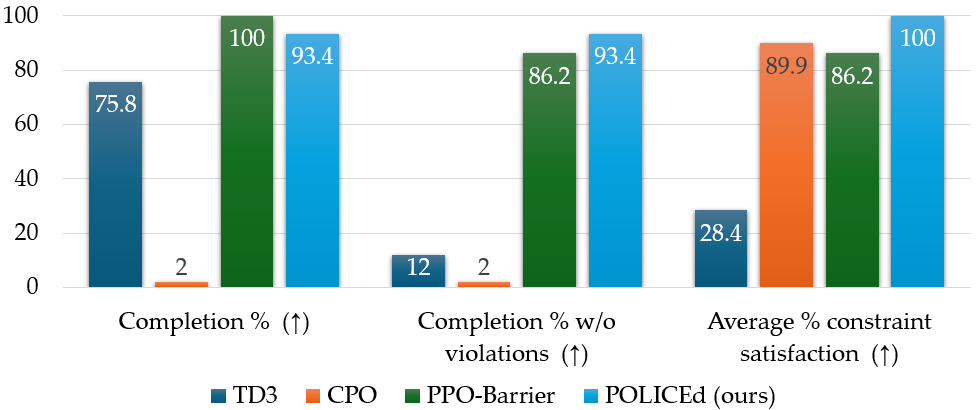
| Models | Completion % (↑) | Completion % w/o violation (↑) | Average reward ± 95% CI (↑) | Average % constraint satisfaction ± 95% CI (↑) |
|---|---|---|---|---|
| POLICEd (ours) | 93.4 | 93.4 | -16.22 ± 0.68 | 100 ± 0.0 |
| TD3 | 75.8 | 12.0 | -45.20 ± 3.23 | 28.4 ± 3.9 |
| CPO | 2.0 | 2.0 | -96.71 ± 3.45 | 89.9 ± 2.7 |
| PPO-Barrier | 100 | 86.2 | -41.26 ± -2.30 | 86.2 ± 3.0 |
| POLICEd trained w/o penalty | 48.0 | 41.6 | -70.09 ± 1.22 | 41.6 ± 4.3 |
| TD3 trained w/o penalty | 99.8 | 48.8 | -45.69 ± 16.61 | 53.4 ± 4.4 |
Table from (Bouvier et al. 2024)
As seen in the table above, our POLICEd policy is the only algorithm to guarantee constraint satisfaction. The soft constraint CPO (Achiam et al. 2017) and the learned safety certificate PPO-Barrier (Yang et al. 2023) baselines provide better constraint adherence than standard RL algorithms like TD3, but still fall far short of guaranteed satisfaction. In comparison, our POLICEd approach has the highest task completion percentage without violations by a 40% margin, while also being the highest reward earning policy by nearly a margin of 3 times.
The ablation study confirms that our POLICEd approach is necessary for constraint satisfaction, as seen by the poor average constraint satisfaction by the TD3 and TD3 trained without penalty policies. As expected, training without penalizing constraint violations is vastly detrimental to the performance of both the TD3 and POLICEd policies. Indeed, the reward shaping is necessary for the POLICEd policy to appropriately tune its affine region to avoid the constraint.
We additionally observed that our POLICEd approach exhibited significantly greater sample efficiency than the other methods. The POLICEd policy converged within 4000 episodes, while PPO-Barrier required nearly twice this amount, and CPO frequently failed to converge after 20,000 episodes.
Conclusion
- Summary. We proposed POLICEd RL, a novel algorithm explicitly designed to enforce hard safety constraints for a black-box robot in closed-loop with a RL policy. Our key insight was to build a repulsive buffer around the unsafe area with a locally affine learned policy to guarantee that trajectories never leave the safe set. Our experiments showed that POLICEd RL can enforce hard constraints in high-dimensional, high-fidelity robotics tasks while significantly outperforming existing soft constraint methods.
- Limitations. As in standard RL, there are no guarantees that the training will converge to a safe policy. Note that this was not an issue in our experiments. Moreover, in high dimensional environments, the number of vertices of buffer region $\mathcal{B}$ can become computationally prohibitive. However, once trained, a POLICEd neural network is just as fast as a standard unconstrained one (Balestriero and LeCun 2023). Finally, if the estimate of the approximation measure $\varepsilon$ is too low, then the safety guarantee of Theorem 1 will not hold. Hence we usually use upper bound of $\varepsilon.$
- Future Directions. We are excited by our findings and believe our method is only the first step towards enforcing hard constraints on RL policy. For future work, we plan to investigate how to enforce multiple constraints simultaneously and study the case of high relative-degree constraints.
References
-
Joshua Achiam, David Held, Aviv Tamar, and Pieter Abbeel, Constrained Policy Optimization, 34th International Conference on Machine Learning (ICML), 2017.
-
Eitan Altman, Constrained Markov Decision Processes, Routledge, 2021.
-
Randall Balestriero and Richard Baraniuk, A spline theory of deep learning, 35th International Conference on Machine Learning (ICML), 2018.
-
Randall Balestriero and Yann LeCun, POLICE: Provably optimal linear constraint enforcement for deep neural networks, IEEE International Conference on Acoustics, Speech and Signal Processing, 2023.
-
Jean-Baptiste Bouvier, Kartik Nagpal, and Negar Mehr, POLICEd RL: Learning Closed-Loop Robot Control Policies with Provable Satisfaction of Hard Constraints, Robotics: Science and Systems (RSS), 2024.
-
Scott Fujimoto, Herke Hoof, and David Meger, Addressing function approximation error in actor-critic methods, International Conference on Machine Learning (ICML), 2018.
-
John Schulman, Filip Wolski, Prafulla Dhariwal, Alec Radford, and Oleg Klimov, Proximal policy optimization algorithms, arXiv preprint arXiv:1707.06347, 2017
-
Yujie Yang, Yuxuan Jiang, Yichen Liu, Jianyu Chen, and Shengbo Eben Li, Model-free safe reinforcement learning through neural barrier certificate, IEEE Robotics and Automation Letters, 2023.