Publications
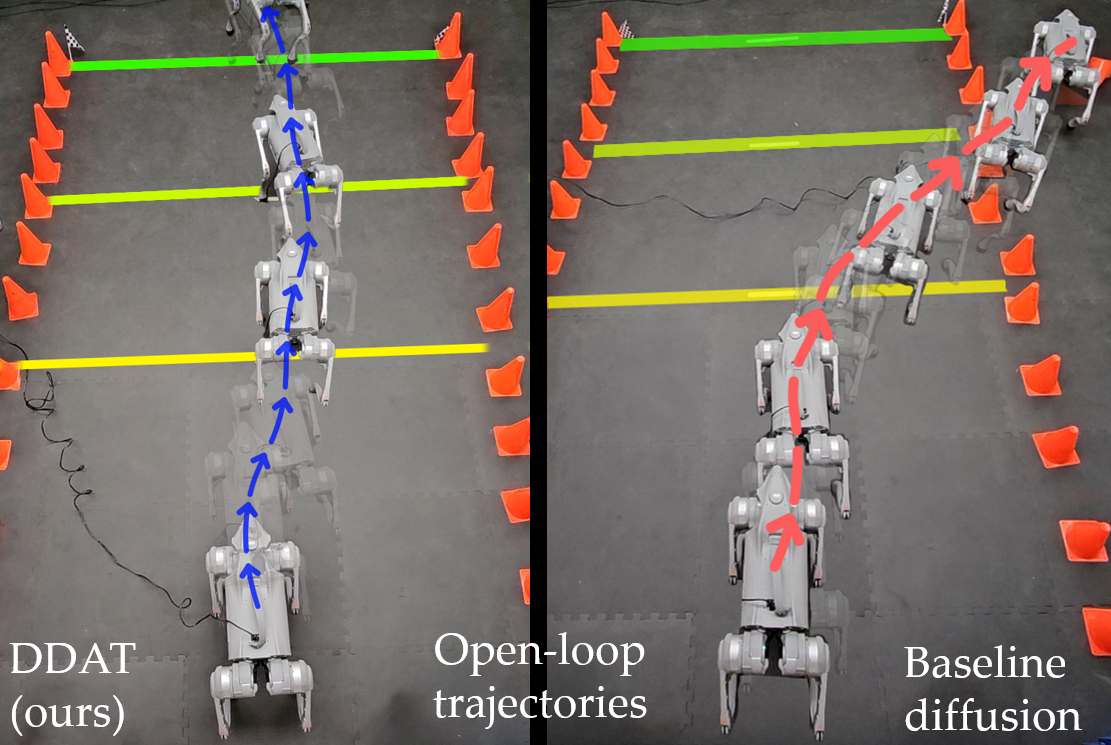
DDAT: Diffusion Policies Enforcing Dynamically Admissible Robot Trajectories
Jean-Baptiste Bouvier, Kanghyun Ryu, Kartik Nagpal, Qiayuan Liao, Koushil Sreenath, Negar Mehr
Robotics: Science and Systems, 2025
Jean-Baptiste Bouvier, Kanghyun Ryu, Kartik Nagpal, Qiayuan Liao, Koushil Sreenath, Negar Mehr
Robotics: Science and Systems, 2025
The stochastic nature of diffusion models prevents them from generating trajectories exactly satisfying the equations of motion of robots.
To alleviate this issue, we introduce DDAT: Diffusion policies for Dynamically Amissible Trajectories.
A trajectory is dynamically admissible if each state belongs to the reachable set of its predecessor by the robot's equations of motion.
To generate such trajectories, our diffusion policies project their predictions onto a dynamically admissible manifold during both training and inference to align the objective of the denoiser neural network with the dynamical admissibility constraint.
Due to the auto-regressive nature of such projections as well as the black-box nature of robot dynamics, exact projections are challenging.
We instead sample a polytopic under-approximation of the reachable set onto which we project the predicted successor, before iterating this process with the projected successor.
By producing accurate trajectories, this projection eliminates the need for diffusion models to continually replan, enabling one-shot long-horizon trajectory planning.
We demonstrate our framework through extensive simulations on a quadcopter and various MuJoCo environments, along with real-world experiments on a Unitree GO1 and GO2.
@inproceedings{bouvier2025ddat,
title = {DDAT: Diffusion Policies Enforcing Dynamically Admissible Robot Trajectories},
author = {Jean-Baptiste Bouvier and Kanghyun Ryu and Kartik Nagpal and Qiayuan Liao and Koushil Sreenath and Negar Mehr},
booktitle = {Robotics: Science and Systems},
year = {2025},
pages = {},
doi = {}
}
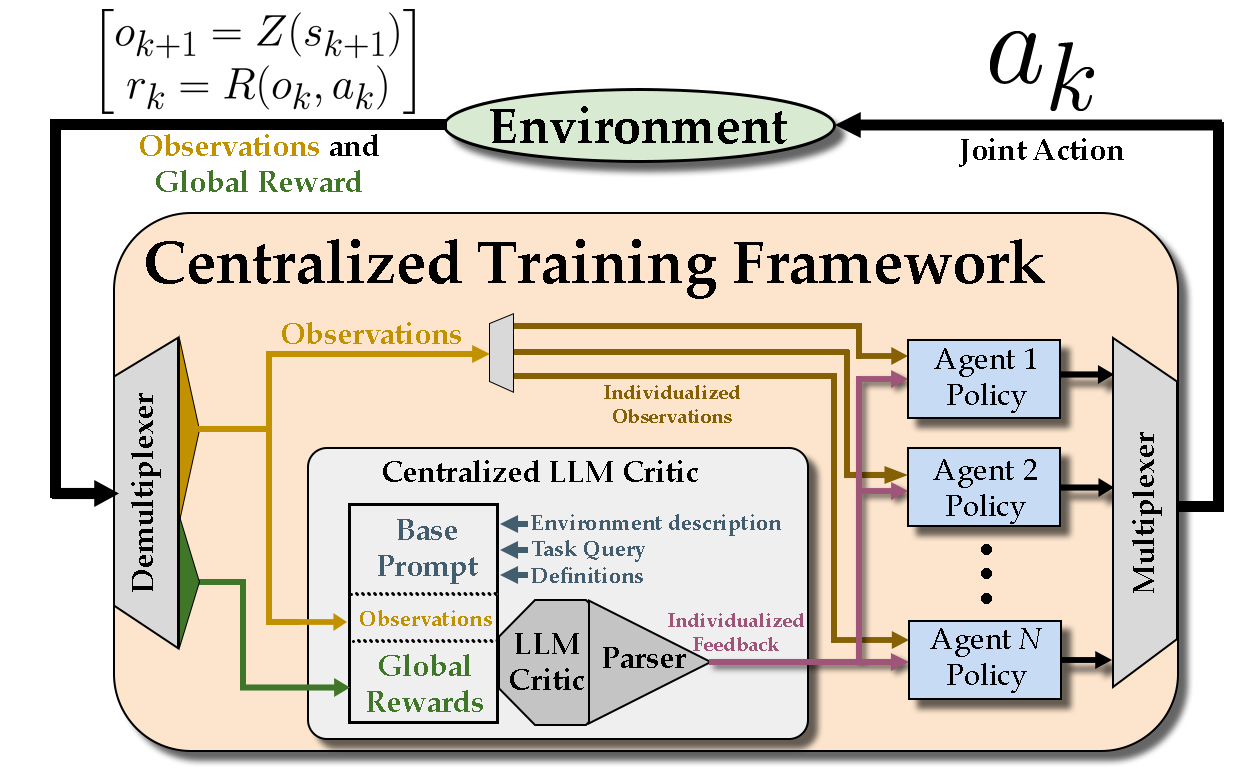
Leveraging Large Language Models for Effective and Explainable Multi-Agent Credit Assignment
Kartik Nagpal, Dayi Dong, Jean-Baptiste Bouvier, Negar Mehr
24th International Conference on Autonomous Agents and Multiagent Systems (AAMAS), 2025
Kartik Nagpal, Dayi Dong, Jean-Baptiste Bouvier, Negar Mehr
24th International Conference on Autonomous Agents and Multiagent Systems (AAMAS), 2025
Recent efforts in autonomous vehicle coordination and in-space assembly have shown the importance of enabling multiple robots collaboration to achieve a shared goal.
A common approach for learning this cooperative behavior is to utilize the centralized-training decentralized-execution paradigm.
However, this approach also introduces a new challenge: how do we evaluate the contributions of each agent's actions to the overall success or failure.
This "credit assignment" problem has been extensively studied in the Multi-Agent Reinforcement Learning (MARL) literature, but with little progress.
In fact, humans performing simple inspection of the agents' trajectories often generate better credit evaluations than existing methods.
We combine this observation with recent works which show Large Language Models (LLMs) demonstrate human-level performance at many pattern recognition tasks.
Our key idea is to reformulate credit assignment as pattern recognition problems and propose our novel Large Language Model Multi-agent Credit Assignment (LLM-MCA) method.
Our approach utilizes a centralized LLM reward-critic which numerically decomposes the overall reward based on the individualized contribution of each agent in the scenario.
We then update the agents' policy networks based on this feedback.
We also propose an extension (LLM-TACA) where our LLM-critic performs explicit task assignment by passing an intermediary goal directly to each agent in the scenario.
Both our methods far outperform the state-of-the-art on a variety of benchmarks, including Level-Based Foraging, Robotic Warehouse, and our new
Spaceworld benchmark which incorporates safety-related constraints.
As an artifact of our methods, we generate large trajectory datasets with each timestep annotated with per-agent reward information, as sampled from our LLM critics.
We hope that by making this dataset available, we will enable future works to directly train a set of collaborative, decentralized policies offline.
@inproceedings{nagpal2024llmca,
title={Leveraging Large Language Models for Effective and Explainable Multi-Agent Credit Assignment},
author={Nagpal, Kartik and Dong, Dayi and Bouvier, Jean-Baptiste and Mehr, Negar},
booktitle = {24th International Conference on Autonomous Agents and Multiagent Systems (AAMAS)},
year={2025}
}

Resilient Trajectory Tracking to Partial Loss of Control Authority over Actuators with Actuation Delay
Jean-Baptiste Bouvier, Himmat Panag, Robyn Woollands, Melkior Ornik
Journal of Guidance, Control, and Dynamics, 2025
Jean-Baptiste Bouvier, Himmat Panag, Robyn Woollands, Melkior Ornik
Journal of Guidance, Control, and Dynamics, 2025
After the loss of control authority over thrusters of the Nauka module, the International Space Station lost attitude control for 45 minutes with potentially disastrous consequences.
Motivated by a scenario of orbital inspection, we consider a similar malfunction occurring to the inspector satellite and investigate whether its mission can still be safely fulfilled.
While a natural approach is to counteract in real-time the uncontrolled and undesirable thrust with the remaining controlled thrusters, vehicles are often subject to actuation delays hindering this approach.
Instead, we extend resilience theory to systems suffering from actuation delay and build a resilient trajectory tracking controller with stability guarantees relying on a state predictor.
We demonstrate that this controller can track accurately the reference trajectory of the inspection mission despite the actuation delay and the loss of control authority over one of the thrusters.
@article{bouvier2023resilient,
title = {Resilient trajectory tracking to partial loss of control authority over actuators with actuation delay},
author = {Jean-Baptiste Bouvier and Himmat Panag and Robyn Woollands and Melkior Ornik},
journal = {Journal of Guidance, Control, and Dynamics},
year = {2025},
volume = {48},
pages = {508 - 519},
doi = {10.2514/1.G007652}
}

Risk-Sensitive Orbital Debris Collision Avoidance using Distributionally Robust Chance Constraints
Kanghyun Ryu, Jean-Baptiste Bouvier, Shaizab Lalani, Siegfried Eggl, Negar Mehr
AIAA SCITECH Forum, 2025
Kanghyun Ryu, Jean-Baptiste Bouvier, Shaizab Lalani, Siegfried Eggl, Negar Mehr
AIAA SCITECH Forum, 2025
The exponential increase in orbital debris and active satellites will lead to congested orbits, necessitating more frequent collision avoidance maneuvers by satellites.
To minimize fuel consumption while ensuring the safety of satellites, enforcing a chance constraint, which poses an upper bound in collision probability with debris, can serve as an intuitive safety measure.
However, accurately evaluating collision probability, which is critical for the effective implementation of chance constraints, remains a non-trivial task.
This difficulty arises because uncertainty propagation in nonlinear orbit dynamics typically provides only limited information, such as finite samples or moment estimates about the underlying arbitrary non-Gaussian distributions.
Furthermore, even if the full distribution were known, it remains unclear how to effectively compute chance constraints with such non-Gaussian distributions.
To address these challenges, we propose a distributionally robust chance-constrained collision avoidance algorithm that provides a sufficient condition for collision probabilities under limited information about the underlying non-Gaussian distribution.
Our distributionally robust approach satisfies the chance constraint for all debris position distributions sharing a given mean and covariance, thereby enabling the enforcement of chance constraints with limited distributional information.
To achieve computational tractability, the chance constraint is approximated using a Conditional Value-at-Risk (CVaR) constraint, which gives a conservative and tractable approximation of the distributionally robust chance constraint.
We validate our algorithm on a real-world inspired satellite-debris conjunction scenario with different uncertainty propagation methods and show that our controller can effectively avoid collisions.
@inproceedings{ryu2025risk,
title={Risk-Sensitive Orbital Debris Collision Avoidance using Distributionally Robust Chance Constraints},
author={Ryu, Kanghyun and Bouvier, Jean-Baptiste and Lalani, Shazaib and Eggl, Siegfried and Mehr, Negar},
booktitle={AIAA SCITECH 2025 Forum},
pages={0758},
year={2025}
}

Learning to Provably Satisfy High Relative Degree Constraints for Black-Box Systems
Jean-Baptiste Bouvier, Kartik Nagpal, Negar Mehr
IEEE Conference on Decision and Control (CDC), 2024
Jean-Baptiste Bouvier, Kartik Nagpal, Negar Mehr
IEEE Conference on Decision and Control (CDC), 2024
In this paper, we develop a method for learning a control policy guaranteed to satisfy an affine state constraint of high relative degree in closed loop with a black-box system.
Previous reinforcement learning (RL) approaches to satisfy safety constraints either require access to the system model, or assume control affine dynamics, or only discourage violations with reward shaping.
Only recently have these issues been addressed with POLICEd RL, which guarantees constraint satisfaction for black-box systems.
However, this previous work can only enforce constraints of relative degree 1.
To address this gap, we build a novel RL algorithm explicitly designed to enforce an affine state constraint of high relative degree in closed loop with a black-box control system.
Our key insight is to make the learned policy be affine around the unsafe set and to use this affine region to dissipate the inertia of the high relative degree constraint.
We prove that such policies guarantee constraint satisfaction for deterministic systems while being agnostic to the choice of the RL training algorithm.
Our results demonstrate the capacity of our approach to enforce hard constraints in the Gym inverted pendulum and on a space shuttle landing simulation.
@inproceedings{bouvier2024learning,
title = {Learning to Provably Satisfy High Relative Degree Constraints for Black-Box Systems},
author = {Jean-Baptiste Bouvier and Kartik Nagpal and Negar Mehr},
booktitle = {IEEE Conference on Decision and Control (CDC)},
year = {2024},
pages = {8320-8325},
doi = {10.1109/CDC56724.2024.10886298}
}

POLICEd RL: Learning Closed-Loop Robot Control Policies with Provable Satisfaction of Hard Constraints
Jean-Baptiste Bouvier, Kartik Nagpal, Negar Mehr
Robotics: Science and Systems (RSS), 2024
Jean-Baptiste Bouvier, Kartik Nagpal, Negar Mehr
Robotics: Science and Systems (RSS), 2024
In this paper, we seek to learn a robot policy guaranteed to satisfy state constraints.
To encourage constraint satisfaction, existing RL algorithms typically rely on Constrained Markov Decision Processes and discourage constraint violations through reward shaping.
However, such soft constraints cannot offer safety guarantees.
To address this gap, we propose POLICEd RL, a novel RL algorithm explicitly designed to enforce affine hard constraints in closed-loop with a black-box environment.
Our key insight is to make the learned policy be affine around the unsafe set and to use this affine region as a repulsive buffer to prevent trajectories from violating the constraint.
We prove that such policies exist and guarantee constraint satisfaction.
Our proposed framework is applicable to both systems with continuous and discrete state and action spaces and is agnostic to the choice of the RL training algorithm.
Our results demonstrate the capacity of POLICEd RL to enforce hard constraints in robotic tasks while significantly outperforming existing methods.
@inproceedings{bouvier2024policed,
title = {POLICEd RL: Learning Closed-Loop Robot Control Policies with Provable Satisfaction of Hard Constraints},
author = {Jean-Baptiste Bouvier and Kartik Nagpal and Negar Mehr},
booktitle = {Robotics: Science and Systems (RSS)},
year = {2024},
pages = {},
doi = {10.15607/RSS.2024.XX.104}
}
Losing Control of your Linear Network? Try Resilience Theory
Jean-Baptiste Bouvier, Sai Pushpak Nandanoori, Melkior Ornik
IEEE Transactions on Control of Network Systems, 2024
Jean-Baptiste Bouvier, Sai Pushpak Nandanoori, Melkior Ornik
IEEE Transactions on Control of Network Systems, 2024
Resilience of cyber-physical networks to unexpected failures is a critical need widely recognized across domains.
For instance, power grids, telecommunication networks, transportation infrastructures and water treatment systems have all been subject to disruptive malfunctions and catastrophic cyber-attacks.
Following such adverse events, we investigate scenarios where a network node suffers a loss of control authority over some of its actuators.
These actuators are not following the controller's commands and are instead producing undesirable outputs.
The repercussions of such a loss of control can propagate and destabilize the whole network despite the malfunction occurring at a single node.
To assess system vulnerability, we establish resilience conditions for networks with a subsystem enduring a loss of control authority over some of its actuators.
Furthermore, we quantify the destabilizing impact on the overall network when such a malfunction perturbs a nonresilient subsystem.
We illustrate our resilience conditions on two academic examples and on the classical IEEE 39-bus system.
@article{bouvier2024losing,
title = {Losing Control of your Linear Network? Try Resilience Theory},
author = {Jean-Baptiste Bouvier and Sai Pushpak Nandanoori and Melkior Ornik},
journal = {IEEE Transactions on Control of Network Systems},
year = {2024},
pages = {1 - 12},
doi = {10.1109/TCNS.2024.3431409}
}
Quantitative Resilience of Generalized Integrators
Jean-Baptiste Bouvier, Kathleen Xu, Melkior Ornik
IEEE Transactions on Automatic Control, 2023
Jean-Baptiste Bouvier, Kathleen Xu, Melkior Ornik
IEEE Transactions on Automatic Control, 2023
When failure is not an option, systems are designed to be resistant to various malfunctions, like a loss of control authority over actuators.
This malfunction consists in some actuators producing uncontrolled and thus possibly undesirable inputs with their full actuation range.
After such a malfunction, a system is deemed resilient if its target is still reachable despite these undesirable inputs.
However, the malfunctioning system might be significantly slower to reach its target compared to its initial capabilities.
To quantify this loss of performance we introduce the notion of quantitative resilience as the maximal ratio over all targets of the minimal reach times for the initial and malfunctioning systems.
Since quantitative resilience is then defined as four nested nonlinear optimization problems, we establish an efficient computation method for control systems with multiple integrators and nonsymmetric input sets.
Relying on control theory and on two specific geometric results we reduce the computation of quantitative resilience to a linear optimization problem.
We illustrate our method on an octocopter.
@article{bouvier2023quantitative,
title = {Quantitative resilience of generalized integrators},
author = {Jean-Baptiste Bouvier and Kathleen Xu and Melkior Ornik},
journal = {IEEE Transactions on Automatic Control},
year = {2023},
volume = {18},
pages = {7591-7600},
doi = {10.1109/TAC.2023.3286942}
}
Resilience of Linear Systems to Partial Loss of Control Authority
Jean-Baptiste Bouvier, Melkior Ornik
Automatica, 2023
Jean-Baptiste Bouvier, Melkior Ornik
Automatica, 2023
After a loss of control authority over thrusters of the Nauka module, the International Space Station lost attitude control for 45 minutes with potentially disastrous consequences.
Motivated by this scenario, we investigate the continued capability of control systems to perform their task despite partial loss of authority over their actuators.
We say that a system is resilient to such a malfunction if for any undesirable inputs and any target state there exists an admissible control driving the state to the target.
Building on controllability conditions and differential games theory, we establish a necessary and sufficient condition for the resilience of linear systems.
As their task might be time-constrained, ensuring completion alone is not sufficient.
We also want to estimate how much slower the malfunctioning system is compared to its nominal performance.
Relying on Lyapunov theory we derive analytical bounds on the reach times of the nominal and malfunctioning systems in order to quantify their resilience.
We illustrate our work on the ADMIRE fighter jet model and on a temperature control system.
@article{bouvier2023resilience,
title = {Resilience of linear systems to partial loss of control authority},
author = {Jean-Baptiste Bouvier and Melkior Ornik},
journal = {Automatica},
year = {2023},
volume = {152},
pages = {110985},
doi = {10.1016/j.automatica.2023.110985}
}
Assured System-Level Resilience for Guaranteed Disaster Response
Melkior Ornik, Jean-Baptiste Bouvier
8th IEEE International Smart Cities Conference, 2022
Melkior Ornik, Jean-Baptiste Bouvier
8th IEEE International Smart Cities Conference, 2022
Resilience of urban infrastructure to sudden, system-wide, potentially catastrophic events is a critical need across domains.
The growing connectivity of infrastructure, including its cyber-physical components which can be controlled in real time, offers an attractive path towards rapid adaptation to adverse events and adjustment of system objectives.
However, existing work in the field often offers piecemeal approaches to particular scenarios.
On the other hand, abstract work on controlled complex systems focuses on attempting to adapt to the changes in the system dynamics or environment, but without understanding that the system may simply not be able to perform its original task after an adverse event.
To address this challenge, this programmatic paper proposes a vision for a new paradigm of infrastructure resilience. Such a framework treats infrastructure across domains through a unified theory of controlled dynamical systems, but remains cognizant of the lack of knowledge about the system following a widespread adverse event and aims to identify the system's fundamental limits.
As a result, it will enable the infrastructure operator to assess and assure system performance following an adverse event, even if the exact nature of the event is not yet known.
Motivated by ongoing work on some facets of the broader problem of assured resilience, in this paper we identify promising early results, challenges that motivate the development of new theory, and possible paths forward for the proposed effort.
@inproceedings{ornik2022assured,
title = {Assured system-level resilience for guaranteed disaster response},
author = {Melkior Ornik and Jean-Baptiste Bouvier},
booktitle = {2022 IEEE International Smart Cities Conference},
year = {2022},
pages = {1 -- 4},
doi = {10.1109/ISC255366.2022.9922438}
}
Resilience of Orbital Inspections to Partial Loss of Control Authority of the Chaser Satellite
Jean-Baptiste Bouvier, Himmat Panag, Robyn Woollands, Melkior Ornik
AAS/AIAA Astrodynamics Specialist Conference, 2022
Jean-Baptiste Bouvier, Himmat Panag, Robyn Woollands, Melkior Ornik
AAS/AIAA Astrodynamics Specialist Conference, 2022
The growing demand for orbital inspections can only be met if these missions guarantee not to endanger the target satellite.
To address this issue we study how to make the chaser satellite resistant to a partial loss of control authority over its thrusters.
This malfunction is characterized by some thrusters of the spacecraft firing in an uncontrolled and thus possibly undesirable manner.
Because of actuation delays, these undesirable thrust inputs cannot be canceled in real-time.
Instead, we first use resilience theory to show that a sufficiently overactuated spacecraft can still reach any location even after losing control of a thruster.
We then calculate the safety distance ensuring that the malfunctioning chaser satellite will not breach the keep-out sphere around the target satellite.
We employ a convex solver to generate a safe minimal-fuel reference trajectory to perform the inspection mission.
Relying on state prediction, adaptive trajectory tracking and PID control the malfunctioning spacecraft is then able to follow the reference trajectory.
We thus demonstrate that an orbital inspection mission can be carried out safely by a spacecraft enduring actuation delay and a loss of control authority over one of its thrusters.
@inproceedings{bouvier2022resilience,
title = {Resilience of Orbital Inspections to Partial Loss of Control Authority over the Chaser Satellite},
author = {Jean-Baptiste Bouvier and Himmat Panag and Robyn Woollands and Melkior Ornik},
booktitle = {2022 AAS/AIAA Astrodynamics Specialist Conference},
year = {2022}
}
Designing Resilient Linear (Driftless) Systems
Jean-Baptiste Bouvier, Melkior Ornik
IEEE Transactions on Automatic Control, 2022
Jean-Baptiste Bouvier, Melkior Ornik
IEEE Transactions on Automatic Control, 2022
Critical systems must be designed resilient to malfunctions and especially to a loss of control authority over actuators.
This malfunction considers actuators producing uncontrolled and possibly undesirable outputs.
We investigate the design of resilient linear systems capable of reaching their target even after such a malfunction.
In contrast with the settings considered by robust control and fault-tolerant control, we consider undesirable but observable inputs of the same magnitude as controls since they are produced by a faulty actuator belonging to the system.
The control inputs can then depend on these undesirable inputs.
Building on our previous work, we focus on designing resilient systems able to withstand the loss of one or multiple actuators.
Since resilience refers to the existence of a control law driving the state to the target, we naturally continue with the synthesis of such a control law.
We conclude with the application of our theory to the ADMIRE fighter jet model.
@article{bouvier2022design,
title = {Designing resilient linear systems},
author = {Jean-Baptiste Bouvier and Melkior Ornik},
journal = {IEEE Transactions on Automatic Control},
year = {2022},
volume = {67},
number = {9},
pages = {4832 -- 4837}
}
Quantitative Resilience of Linear Systems
Jean-Baptiste Bouvier, Melkior Ornik
20th European Control Conference, 2022
Jean-Baptiste Bouvier, Melkior Ornik
20th European Control Conference, 2022
Actuator malfunctions may have disastrous consequences for systems not designed to mitigate them.
We focus on the loss of control authority over actuators, where some actuators are uncontrolled but remain fully capable.
To counteract the undesirable outputs of these malfunctioning actuators, we use real-time measurements and redundant actuators.
In this setting, a system that can still reach its target is deemed resilient.
To quantify the resilience of a system, we compare the shortest time for the undamaged system to reach the target with the worst-case shortest time for the malfunctioning system to reach the same target, i.e., when the malfunction makes that time the longest.
Contrary to prior work on driftless linear systems, the absence of analytical expression for time-optimal controls of general linear systems prevents an exact calculation of quantitative resilience.
Instead, relying on Lyapunov theory we derive analytical bounds on the nominal and malfunctioning reach times in order to bound quantitative resilience.
We illustrate our work on a temperature control system.
@inproceedings{bouvier2022quantitative_ECC,
title = {Quantitative resilience of linear systems},
author = {Jean-Baptiste Bouvier and Melkior Ornik},
booktitle = {20th European Control Conference},
year = {2022},
pages = {485 -- 490},
doi = {10.23919/ECC55457.2022.9838147}
}
The Maximax Minimax Quotient Theorem
Jean-Baptiste Bouvier, Melkior Ornik
Journal of Optimization Theory and Applications, 2022
Jean-Baptiste Bouvier, Melkior Ornik
Journal of Optimization Theory and Applications, 2022
We present an optimization problem emerging from optimal control theory and situated at the intersection of fractional programming and linear max-min programming on polytopes.
A naive solution would require solving four nested, possibly nonlinear, optimization problems.
Instead, relying on numerous geometric arguments we determine an analytical solution to this problem.
In the course of proving our main theorem we also establish another optimization result stating that the minimum of a specific minimax optimization is located at a vertex of the constraint set.
@article{bouvier2022maximax,
title = {The maximax minimax quotient theorem},
author = {Jean-Baptiste Bouvier and Melkior Ornik},
journal = {Journal of Optimization Theory and Applications},
year = {2022},
volume = {192},
pages = {1084 -- 1101},
publisher = {Springer},
doi = {10.1007/s10957-022-02008-z}
}
Distributed Transient Safety Verification via Robust Control Invariant Sets: A Microgrid Application
Jean-Baptiste Bouvier, Sai Pushpak Nandanoori, Melkior Ornik, Soumya Kundu
American Control Conference, 2022
Jean-Baptiste Bouvier, Sai Pushpak Nandanoori, Melkior Ornik, Soumya Kundu
American Control Conference, 2022
Modern safety-critical energy infrastructures are operated in a hierarchical and modular control framework allowing only limited data exchange between modules.
In this context, to assure system-wide safety each module must synthesize and communicate constraints on the values of exchanged data.
To ensure transient safety in inverter-based microgrids, we develop a set invariance-based distributed safety verification algorithm for each inverter module.
Applying Nagumo's invariance condition, we construct a robust polynomial optimization problem to jointly search for safety-admissible set of control set-points and design parameters, under allowable disturbances from neighbors.
We solve the verification problem with sum-of-squares programming and we perform numerical simulations using grid-forming inverters to illustrate our method.
@inproceedings{bouvier2022distributed,
title = {Distributed transient safety verification via robust control invariant sets: a microgrid application},
author = {Jean-Baptiste Bouvier and Sai Pushpak Nandanoori and Melkior Ornik and Soumya Kundu},
booktitle = {2022 American Control Conference},
year = {2022},
pages = {2202 -- 2207},
doi = {10.23919/ACC53348.2022.9867323}
}
Quantitative Resilience of Linear Driftless Systems
Jean-Baptiste Bouvier, Kathleen Xu, Melkior Ornik
SIAM Conference on Control and its Applications, 2021
Jean-Baptiste Bouvier, Kathleen Xu, Melkior Ornik
SIAM Conference on Control and its Applications, 2021
This paper introduces the notion of quantitative resilience of a control system.
Following prior work, we study linear driftless systems enduring a loss of control authority over some of their actuators.
Such a malfunction results in actuators producing possibly undesirable inputs over which the controller has real-time readings but no control.
By definition, a system is resilient if it can still reach a target after a partial loss of control authority.
However, after such a malfunction, a resilient system might be significantly slower to reach a target compared to its initial capabilities.
We quantify this loss of performance through the new concept of quantitative resilience.
We define such a metric as the maximal ratio of the minimal times required to reach any target for the initial and malfunctioning systems.
Naive computation of quantitative resilience directly from the definition is a complex task as it requires solving four nested, possibly nonlinear, optimization problems.
The main technical contribution of this work is to provide an efficient method to compute quantitative resilience.
Relying on control theory and on two novel geometric results we reduce the computation of quantitative resilience to a single linear optimization problem.
We demonstrate our method on an opinion dynamics scenario.
@inproceedings{bouvier2021quantitative,
title = {Quantitative resilience of linear driftless systems},
author = {Jean-Baptiste Bouvier and Kathleen Xu and Melkior Ornik},
booktitle = {SIAM Conference on Control and its Applications},
year = {2021},
pages = {32 -- 39},
doi = {10.1137/1.9781611976847.5}
}
Resilient Reachability for Linear Systems
Jean-Baptiste Bouvier, Melkior Ornik
21st IFAC World Congress, 2020
Jean-Baptiste Bouvier, Melkior Ornik
21st IFAC World Congress, 2020
A fault-tolerant system is able to reach its goal even when some of its components are malfunctioning.
This paper examines tolerance to a specific type of malfunction: the loss of control authority over actuators.
Namely, we investigate whether the desired target set for a linear system remains reachable even after such a loss of authority.
We frame this problem as the verification of whether a set is reachable from a certain initial state under any undesirable input, without prior knowledge of future undesirable inputs.
Building on previous work on reachability with undesirable inputs, this paper develops a reachability condition for linear systems, and obtains a formula that describes reachability of the goal set for driftless linear systems by computing minimum of a concave-convex objective function.
From this formulation we establish two novel sufficient conditions for reachability of the goal set.
@inproceedings{bouvier2020resilient,
title = {Resilient reachability for linear systems},
author = {Jean-Baptiste Bouvier and Melkior Ornik},
booktitle = {21st IFAC World Congress},
pages = {4409 -- 4414},
year = {2020},
doi = {10.1016/j.ifacol.2020.12.372}
}
Spacecraft Trajectory Tracking and Parameter Estimation around a Splitting Contact Binary Asteroid
Tiago Silva, Jean-Baptiste Bouvier, Kathleen Xu, Masatoshi Hirabayashi, Koki Ho
Acta Astronautica, 2020
Tiago Silva, Jean-Baptiste Bouvier, Kathleen Xu, Masatoshi Hirabayashi, Koki Ho
Acta Astronautica, 2020
Increasing interest in asteroid mining and in-situ resource utilization will lead to an increase in asteroid surface operations.
The geophysical properties of asteroids are often unknown and play a significant role in the resulting gravitational fields.
Surface operations such as mining may significantly alter the asteroid's structure or, in the case of contact binary asteroids, cause the asteroid to split depending on the rotational condition.
The coupled problem of estimating unknown parameters of a splitting contact-binary system and controlling a spacecraft's trajectory in the system's vicinity is investigated.
An indirect adaptive control scheme is utilized to simultaneously meet both objectives.
The results are compared with the traditional 2-body controller and the improvement enabled by the proposed scheme is demonstrated.
@article{splitting_asteroid,
title = {Spacecraft trajectory tracking and parameter estimation around a splitting contact binary asteroid},
author = {Silva, Tiago and Bouvier, Jean-Baptiste and Xu, Kathleen and Hirabayashi, Masatoshi and Ho, Koki},
journal = {Acta Astronautica},
volume = {171},
pages = {280 -- 289},
year = {2020},
publisher = {Elsevier},
doi ={10.1016/j.actaastro.2020.02.052}
}
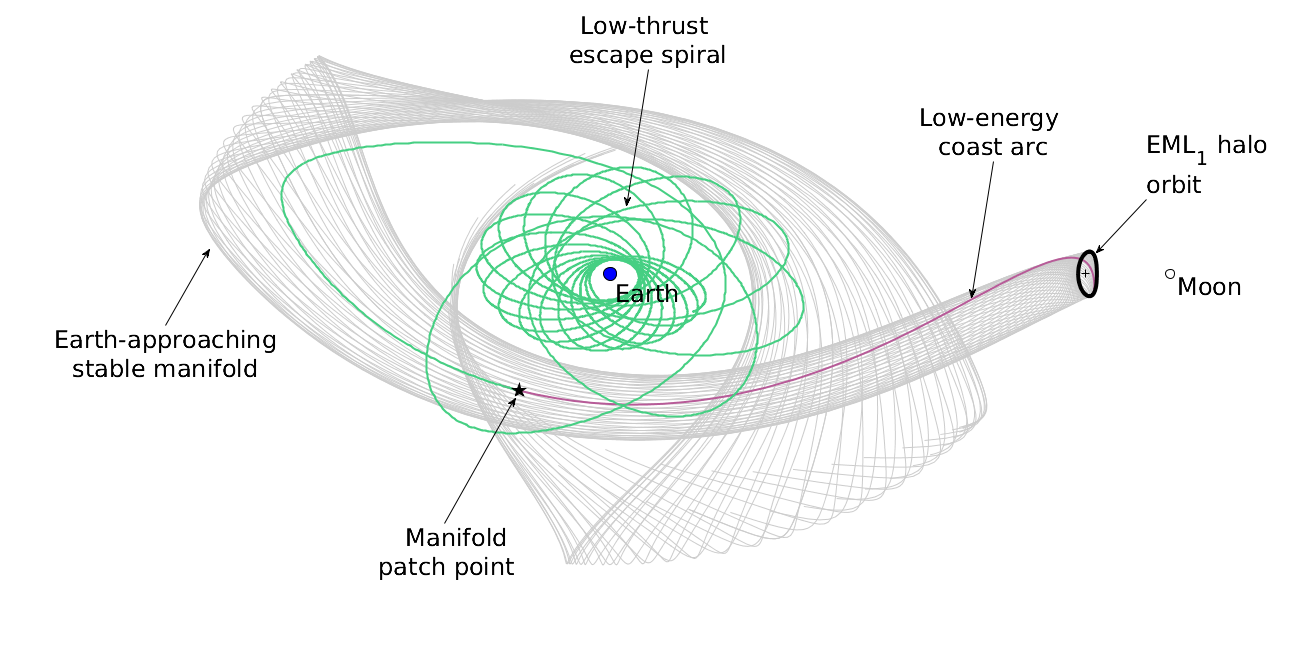
Preliminary Design of Low-Energy, Low-Thrust Transfers to Halo Orbits using Feedback Control
Bindu Jagannatha, Jean-Baptiste Bouvier, Koki Ho
Journal of Guidance, Control and Dynamics, 2019
Bindu Jagannatha, Jean-Baptiste Bouvier, Koki Ho
Journal of Guidance, Control and Dynamics, 2019
Calculating low-thrust trajectories that connect geocentric orbits to Earth-moon halo orbits involves designing the many-revolution thrust arc required to depart Earth vicinity.
Existing methods are based on solving the corresponding optimal control problem and hence are computationally expensive, involve providing hard-to-obtain initial guesses, and do not lend themselves well to quick parametric trade studies.
In this paper, a stochastic optimization algorithm is coupled with a Lyapunov feedback control law to explore the solution space for designing Earth-to-halo low-energy low-thrust trajectories.
While the objective is to minimize the fuel consumed for the transfer, the time of flight is constrained so as to optimally distribute the coast time between the low-thrust escape spiral and the low-energy arc.
Engines are assumed to have a constant specific impulse and provide constant thrust throughout the transfer. The results obtained from this method are then compared with other available reference solutions in order to quantify its effectiveness in designing such transfers.
Favorable comparisons thus obtained demonstrate the utility of the proposed method in calculating almost-optimal solutions, combined with a large improvement in computation time.
@article{bindu2019preliminary,
author = {Jagannatha, Bindu B. and Bouvier, Jean-Baptiste and Ho, Koki},
title = {Preliminary design of low-energy, low-thrust transfers to halo orbits using feedback control},
journal = {Journal of Guidance, Control, and Dynamics},
volume = {42},
number = {2},
pages = {260-271},
year = {2019},
doi = {10.2514/1.G003759}
}
Strategies for Space Rendezvous on Lunar Distant Retrograde Orbits
Jean-Baptiste Bouvier, Williams Zanga, Bastien Le Bihan, Stephanie Lizy-Destrez
ISAE Supaero, 2017
Jean-Baptiste Bouvier, Williams Zanga, Bastien Le Bihan, Stephanie Lizy-Destrez
ISAE Supaero, 2017
This research is motivated by a possible deployment of an inhabited space station on a cislunar orbit.
This paper describes space rendezvous on Lunar Distant Retrograde Orbits (DRO).
More precisely, the core study of this research tackles the construction of a DRO, and the rendezvous itself.
Then further work has been conducted including safety analysis during the rendezvous operations and optimization of DRO computation.
Theses
Guaranteed Resilience of Autonomous Systems to Loss of Control Authority over Actuators
Jean-Baptiste Bouvier Advisor: Melkior Ornik
Doctoral thesis. University of Illinois Urbana-Champaign, 2023
Jean-Baptiste Bouvier Advisor: Melkior Ornik
Doctoral thesis. University of Illinois Urbana-Champaign, 2023
After docking to the International Space Station (ISS), the Nauka module suffered a software error causing its thrusters to misfire.
In turn, these uncontrolled thrusters rotated the whole space station by 540° before being counteracted by other thrusters of the ISS.
Motivated by such a scenario, this thesis investigates the guaranteed resilience of autonomous systems to a similar class of malfunctions called partial loss of control authority over actuators.
These malfunctions are characterized by actuators producing uncontrolled and undesirable outputs instead of following the controller’s commands.
A loss of control authority can be caused, for instance, by a software bug as in the ISS example or by an adversarial takeover of some actuators of the system.
In this setting, we investigate the malfunctioning system's remaining capabilities to complete its mission in terms of resilient reachability and resilient trajectory tracking.
We also quantify the resilience of linear systems by comparing the reachability performance of the nominal dynamics with that of the worst-case malfunctioning dynamics.
We extend our resilience investigation to systems further inflicted with actuation delays preventing an immediate cancellation of the undesirable outputs.
We illustrate our theory on a wide range of applications including an octocopter, a fighter jet model, and an orbital inspection mission.
@phdthesis{bouvier2023phd,
author = {Jean-Baptiste Bouvier},
title = {Guaranteed resilience of autonomous systems to loss of control authority over actuators},
school = {University of Illinois Urbana-Champaign},
year = {2023}
}
Orbit Control for a Spacecraft around a Splitting Contact Binary Asteroid
Jean-Baptiste Bouvier Advisor: Koki Ho
Master thesis. University of Illinois Urbana-Champaign, 2018
Jean-Baptiste Bouvier Advisor: Koki Ho
Master thesis. University of Illinois Urbana-Champaign, 2018
This thesis examines an orbit control problem for a spacecraft around a contact binary asteroid considering the dynamics of both the spacecraft and the asteroid itself.
It is known that approximately 15\% of the near-Earth asteroids are binary, and among these the fraction of contact binaries is between 6 and 10\%.
Most contact binary asteroids are constituted of an agglomeration of smaller boulders maintained together due to their internal gravity, which is a relatively unstable configuration.
Therefore, even a minor change in their mass distribution, like would be caused by the landing of mining machines, can result in a modification of the asteroid's structure including a landslide or a splitting.
Particularly, separation of the asteroid into two parts is problematic in terms of orbit control, because of the consequences on the gravitational field of the asteroid.
Traditional two-body orbital control methods cannot be applied to the missions to those asteroids because they do not consider the dynamic activities of the asteroids themselves.
This thesis proposes and evaluates a control method to follow a predefined path under unknown states of the splitting binary asteroid.
@mastersthesis{bouvier2018msc,
author = {Jean-Baptiste Bouvier},
title = {Orbit control for a spacecraft around a splitting contact binary asteroid},
school = {University of Illinois Urbana-Champaign},
year = {2018}
}